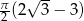/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoboczny/Pole

Zadanie nr 8263017

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkąt równoboczny wpisane są 3 koła o równych promieniach, przy czym każde koło jest styczne do dwóch boków trójkąta oraz do dwóch pozostałych kół. Oblicz stosunek sumy pól tych kół do pola trójkąta.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy promienie tych kół przez r a bok trójkąta przez a .

PIC

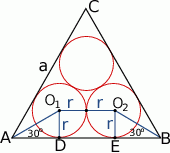
Z trójkąta prostokątnego 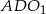ADO 1 mamy

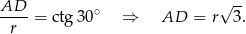
√ -- AD-- = ctg 30∘ ⇒ AD = r 3. r

Podobnie 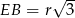√ -- EB = r 3 . Mamy zatem

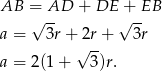
AB =√ AD + DE √+-EB a = 3r + 2r + 3r √ -- a = 2(1 + 3)r.

Pole trójkąta jest więc równe

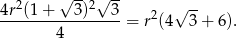
√ -- √ -- 4r2(1-+---3)2--3- 2 √ -- 4 = r(4 3+ 6).

Liczymy teraz szukany iloraz pól

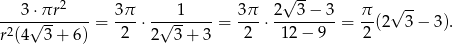
√ -- ---3-⋅πr2---- 3π- ---1----- 3π- 2---3−--3 π- √ -- r2(4√ 3-+ 6) = 2 ⋅ 2√ 3+ 3 = 2 ⋅ 12− 9 = 2(2 3 − 3 ).

 
Odpowiedź: √ -- π-(2 3 − 3) 2

Wersja PDF