/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoboczny/Pole

Zadanie nr 9624248

Podstawą trójkąta równobocznego jest średnica koła. Oblicz stosunek pola części trójkąta leżącej na zewnątrz koła do pola części trójkąta leżącej wewnątrz koła.

Wersja PDF

Rozwiązanie

Zacznijmy od rysunku.

PIC

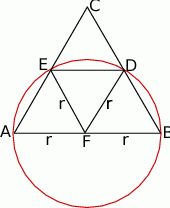
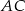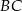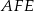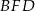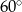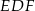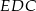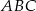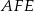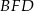Zauważmy, że jeżeli połączymy środek okręgu z punktami przecięcia boków AC i BC z okręgiem, to trójkąty AF E i BF D są równoramienne oraz mają kąt przy podstawie równy 60∘ . Zatem są równoboczne. To oznacza, że równoboczne są również trójkąty EDF i EDC . Aby policzyć część pola trójkąta ABC znajdującą się wewnątrz koła, musimy dodać do siebie pola dwóch małych trójkątów AF E i BF D , oraz wycinka kołowego 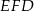EF D , który stanowi 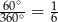60∘∘ = 1 360 6 pola całego koła. Liczymy

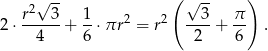
√ -- ( √ -- ) r2 3 1 3 π 2⋅ -----+ --⋅πr 2 = r2 ----+ -- . 4 6 2 6

Pole całego trójkąta 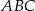ABC jest równe

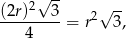
√ -- (2r-)2-3- 2√ -- 4 = r 3,

zatem szukany iloraz wynosi:

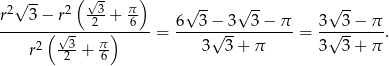
√ -- (√ - ) r2 3 − r2 -23+ π6- 6√ 3− 3√ 3− π 3√ 3-− π ------(√-------)-----= ----√-----------= -√-------. r2 --3+ π- 3 3 + π 3 3 + π 2 6

 
Odpowiedź: 3√ 3−π 3√-3+π

Wersja PDF