Zadanie nr 1630530
W trójkąt prostokątny 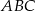 o przyprostokątnych długości
o przyprostokątnych długości 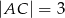 i
i 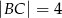 wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków
wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków  i
i 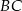 , a drugi do boków
, a drugi do boków 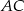 i
i 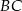 .
.
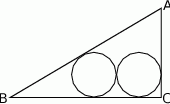
Oblicz długość promienia tych okręgów.
Rozwiązanie
Niech  oznacza środek okręgu stycznego do przeciwprostokątnej i niech
oznacza środek okręgu stycznego do przeciwprostokątnej i niech  będzie punktem styczności tego okręgu z bokiem
będzie punktem styczności tego okręgu z bokiem  .
.
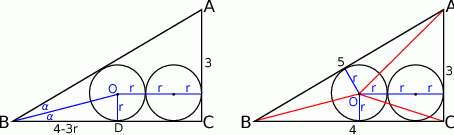
Punkt 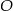 leży na dwusiecznej kąta
leży na dwusiecznej kąta 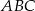 , więc jeżeli oznaczymy
, więc jeżeli oznaczymy 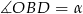 to
to 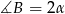 . Jeżeli przez
. Jeżeli przez  oznaczymy szukaną długość promienia to łatwo wyliczyć przyprostokątne trójkąta prostokątnego
oznaczymy szukaną długość promienia to łatwo wyliczyć przyprostokątne trójkąta prostokątnego 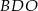 :
: 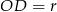 i
i 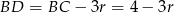 . Widać teraz, że aby wyliczyć
. Widać teraz, że aby wyliczyć  wystarczy wyliczyć
wystarczy wyliczyć 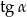 . Zrobimy to na dwa sposoby.
. Zrobimy to na dwa sposoby.
Sposób I
Korzystając ze wzoru
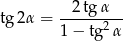
mamy
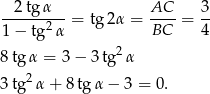
Podstawiamy 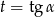 .
.
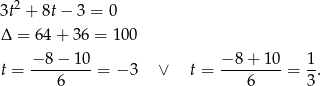
Ujemne rozwiązanie odrzucamy i mamy 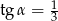 . Stąd
. Stąd
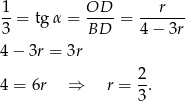
Sposób II
Jeżeli nie chcemy korzystać ze wzoru na 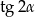 to wystarczy nam wzór
to wystarczy nam wzór
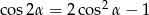
Mamy z niego
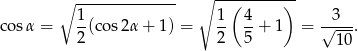
Z jedynki trygonometrycznej wyliczamy sinus
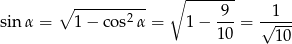
Zatem
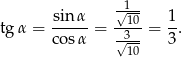
Promień wyliczamy jak poprzednio.
Sposób III
Tym razem obejdziemy się bez trygonometrii. Jeżeli połączymy punkt  z wierzchołkami trójkąta to otrzymamy trzy trójkąty
z wierzchołkami trójkąta to otrzymamy trzy trójkąty 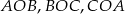 . Suma ich pól musi być równa polu trójkąta, co daje równanie
. Suma ich pól musi być równa polu trójkąta, co daje równanie
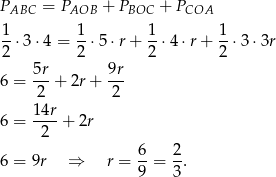
Sposób IV
Tym razem poprowadźmy odcinek 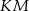 prostopadły do boku
prostopadły do boku 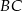 i styczny do obu okręgów.
i styczny do obu okręgów.
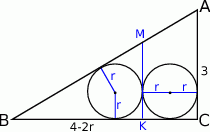
Obliczymy długości wszystkich boków trójkąta 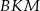 , co pozwoli wyliczyć promień okręgu wpisanego w ten trójkąt ze wzoru na pole.
, co pozwoli wyliczyć promień okręgu wpisanego w ten trójkąt ze wzoru na pole.
Z podobieństwa trójkątów 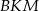 i
i 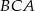 mamy
mamy
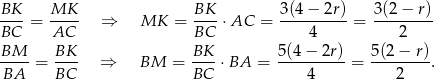
Możemy teraz na dwa sposoby obliczyć pole trójkąta  . Z jednej strony jest ono równe
. Z jednej strony jest ono równe
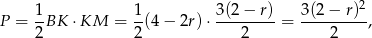
a z drugiej
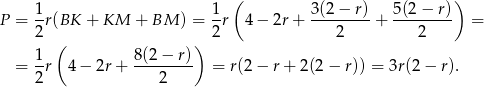
Mamy zatem równanie
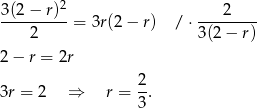
Odpowiedź: 

