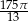/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Promień okręgu

Zadanie nr 4023675

Dodaj do ulubionych
Dodaj do rozwiązanych

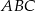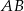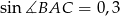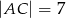Dany jest trójkąt prostokątny ABC o przeciwprostokątnej AB , taki że sin ∡BAC = 0,3 i |AC | = 7 . Oblicz pole koła opisanego na tym trójkącie.

Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

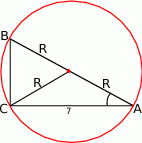
Z podanego sinusa łatwo obliczyć cosinus:

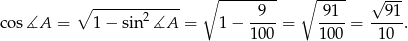
∘ ------------ ∘ -------- ∘ ---- √ --- 2 -9-- 91-- --91- cos ∡A = 1− sin ∡A = 1 − 10 0 = 100 = 10 .

Sposób I

Na mocy twierdzenia sinusów mamy

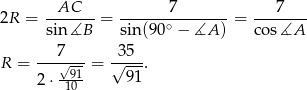
AC 7 7 2R = ------- = -------∘------- = -------- sin∡B sin(90 − ∡A ) cos∡A ---7--- -35-- R = √-91-= √ ---. 2 ⋅ 10 91

Zatem pole koła opisanego na trójkącie 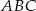ABC jest równe

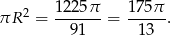
πR 2 = 1225π--= 175π-. 91 13

Sposób II

Tym razem obejdziemy się bez twierdzenia sinusów. Mając obliczony 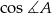cos∡A możemy obliczyć długość przeciwprostokątnej.

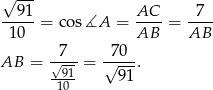
√ --- --91-= co s∡A = AC--= -7-- 10 AB AB -7-- -7-0- AB = √-91 = √ --. 10 91

Teraz wystarczy zauważyć, że promień okręgu opisanego na trójkącie prostokątnym to dokładnie połowa długości przeciwprostokątnej – tak jest, bo przeciwprostokątna jest średnicą tego okręgu. Zatem

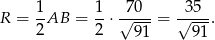
1- 1- -70-- -35-- R = 2 AB = 2 ⋅ √ 91-= √ 91.

Pole koła liczymy jak w pierwszym sposobie.  
Odpowiedź: 175π 13

Wersja PDF