/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Promień okręgu

Zadanie nr 4652281

Dwusieczna kąta prostego w trójkącie prostokątnym dzieli przeciwprostokątna w stosunku 3:4. Oblicz stosunek pola koła opisanego na tym trójkącie do pola koła wpisanego w ten trójkąt.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

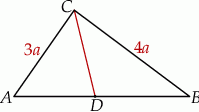
Na mocy twierdzenia o dwusiecznej mamy

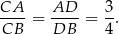
CA--= AD-- = 3-. CB DB 4

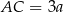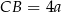Zatem AC = 3a i CB = 4a dla pewnego a . W takim razie na mocy twierdzenia Pitagorasa mamy

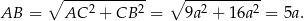
∘ ------------ ∘ ----------- AB = AC 2 + CB 2 = 9a2 + 16a2 = 5a.

Promień okręgu opisanego na trójkącie prostokątnym to dokładnie połowa przeciwprostokątnej, czyli

R = 5a. 2

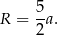
Sposób I

Aby wyliczyć promień okręgu wpisanego, skorzystamy ze wzoru na pole 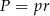P = pr , gdzie 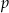p –połowa obwodu.

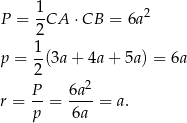
1 P = -CA ⋅CB = 6a2 2 p = 1(3a + 4a + 5a) = 6a 2 P 6a2 r = -- = ----= a. p 6a

Szukany iloraz pól wynosi więc

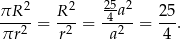
2 2 25 2 πR---= R-- = 4-a--= 25. πr 2 r2 a2 4

Sposób II

Tym razem skorzystamy ze wzoru

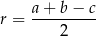
a+--b−-c- r = 2

na promień okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości 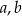a,b i przeciwprostokątnej c . W naszej sytuacji mamy

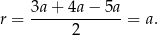
3a-+-4a-−--5a r = 2 = a.

Szukany iloraz pól wynosi więc

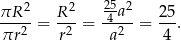
πR 2 R 2 245a2 25 ---2-= --2 = --2--= --. πr r a 4

 
Odpowiedź: 25 4

Wersja PDF