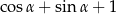/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Promień okręgu

Zadanie nr 9169226

Dodaj do ulubionych
Dodaj do rozwiązanych

Jeden z kątów ostrych trójkąta prostokątnego ma miarę α . Oblicz stosunek wysokości poprowadzonej z wierzchołka kąta prostego do promienia okręgu wpisanego w ten trójkąt.

Rozwiązanie

Zaczynamy od rysunku.

PIC

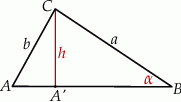
Długość okręgu wpisanego obliczamy ze wzoru na pole 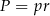P = pr , gdzie 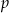p – połowa obwodu trójkąta.

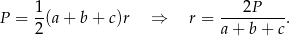
P = 1(a + b + c)r ⇒ r = ---2P----. 2 a + b + c

Długość wysokości również obliczamy ze wzoru na pole

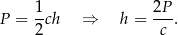
P = 1ch ⇒ h = 2P-. 2 c

Zatem iloraz wynosi

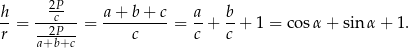
2P h-= --c---= a-+-b-+-c = a+ b-+ 1 = co sα + sinα + 1 . r --2P-- c c c a+b+c

 
Odpowiedź: co sα + sin α+ 1

Wersja PDF