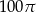/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Promień okręgu

Zadanie nr 9419738

Przyprostokątna trójkąta prostokątnego ma długość 10. Miara kąta ostrego leżącego naprzeciw tej przyprostokątnej wynosi 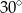30∘ . Oblicz pole koła opisanego na tym trójkącie.

Wersja PDF

Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

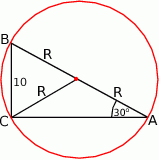
Sposób I

Zauważmy, że promień okręgu opisanego na trójkącie prostokątnym to dokładnie połowa długości przeciwprostokątnej – tak jest, bo przeciwprostokątna jest średnicą tego okręgu. Zatem

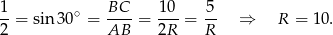
1- ∘ BC-- 10- 5- 2 = sin 30 = AB = 2R = R ⇒ R = 10.

Pole koła opisanego na trójkącie 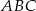ABC jest więc równe

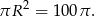
πR 2 = 100π .

Sposób II

Na mocy twierdzenia sinusów mamy

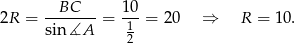
BC 1 0 2R = ------- = -1- = 20 ⇒ R = 10 . sin∡A 2

Pole koła liczymy jak w pierwszym sposobie.  
Odpowiedź: 100 π

Wersja PDF