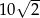Zadanie nr 9687080
W trójkącie prostokątnym 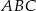 przyprostokątne mają długości
przyprostokątne mają długości 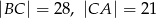 . Na boku
. Na boku 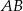 wybrano punkt
wybrano punkt 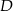 tak, że pole trójkąta
tak, że pole trójkąta 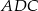 jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie
jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie 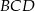 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
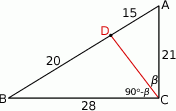
Obliczmy długość przeciwprostokątnej
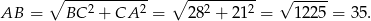
Zauważmy, że z podanego pola trójkąta 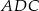 łatwo jest obliczyć długość odcinka
łatwo jest obliczyć długość odcinka 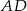 – korzystamy ze wzoru na pole z sinusem.
– korzystamy ze wzoru na pole z sinusem.
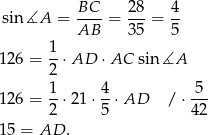
Stąd
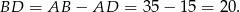
Sposób I
Korzystamy z twierdzenia cosinusów. Korzystając z tego twierdzenia obliczamy długość odcinka 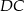 .
.
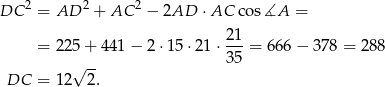
Teraz korzystamy z twierdzenia sinusów w trójkącie 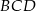 .
.
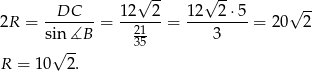
Sposób II
Stosując twierdzenie sinusów w trójkątach 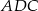 i
i 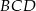 mamy
mamy
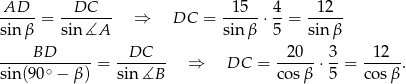
To oznacza, że 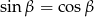 , czyli
, czyli 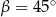 . Zatem raz jeszcze stosując twierdzenie sinusów w trójkącie
. Zatem raz jeszcze stosując twierdzenie sinusów w trójkącie 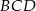 mamy
mamy
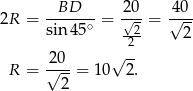
Odpowiedź: