Zadanie nr 1101814
Trójkąty 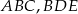 i
i 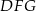 są równoboczne oraz
są równoboczne oraz 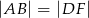 . Punkty
. Punkty 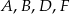 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 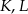 i
i 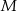 są środkami odcinków
są środkami odcinków 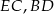 i
i 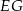 . Wykaż, że punkty
. Wykaż, że punkty 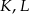 i
i 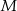 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
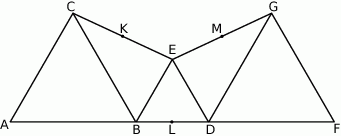
Rozwiązanie
Dorysujmy trójkąt 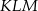 .
.
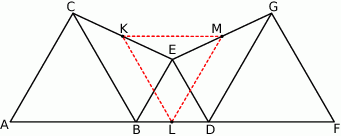
Zauważmy, że odcinek 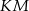 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 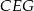 , jest więc równoległy do odcinka
, jest więc równoległy do odcinka 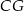 , a ten z kolei jest równoległy do prostej
, a ten z kolei jest równoległy do prostej 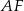 (bo z założenia trójkąty
(bo z założenia trójkąty 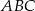 i
i 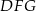 są przystające).
są przystające).
Popatrzmy teraz na odcinek 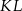 . Jest to odcinek łączący środki ramion w trapezie
. Jest to odcinek łączący środki ramion w trapezie 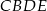 , czyli jest równoległy do podstaw tego trapezu (zamiast korzystać z własności trapezu mogliśmy skorzystać z twierdzenia odwrotnego do twierdzenia Talesa). Zatem
, czyli jest równoległy do podstaw tego trapezu (zamiast korzystać z własności trapezu mogliśmy skorzystać z twierdzenia odwrotnego do twierdzenia Talesa). Zatem 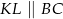 . W szczególności
. W szczególności
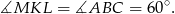
Podobnie (patrząc na odcinek 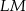 w trapezie
w trapezie 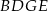 ) uzasadniamy, że
) uzasadniamy, że 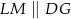 . Stąd
. Stąd
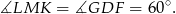
Uzasadniliśmy, że dwa kąty trójkąta 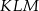 mają miarę
mają miarę 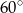 . To oznacza, że jest to trójkąt równoboczny.
. To oznacza, że jest to trójkąt równoboczny.

