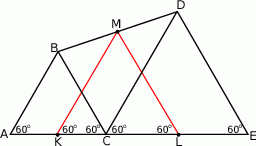
Zadanie nr 3995690
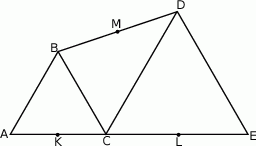
Trójkąty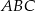 
i 
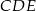są równoboczne. Punkty 
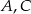i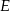 
leżą na jednej prostej. Punkty 
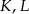i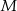 
są środkami odcinków 
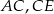i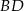 
(zobacz rysunek). Wykaż, że punkty 
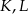i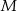 
są wierzchołkami trójkąta równobocznego.
Rozwiązanie
Dorysujmy odcink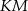i 
i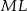 
.
Zauważmy, że oba odcink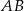i 
i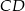 
tworzą z prostą 
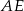kąt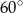 
, czyli są do siebie równoległe. Zatem na mocy twierdzenia Talesa, odcinek 
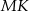łączący środki odcinków 
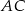i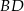 
jest równoległy do 
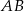i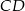 
. Zatem 
.
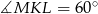Podobnie, patrząc na odcink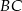i 
i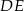 
, uzasadniamy, że odcinek 
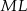jest równoległy do 
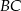i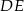 
. Zatem 
.
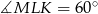Skoro dwa kąty trójkąta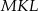 
są równe 
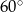, to musi to być trójkąt równoboczny.
