Zadanie nr 9900662
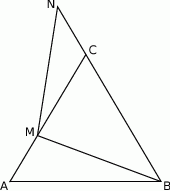
Trójkąt 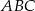 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 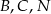 są współliniowe. Na boku
są współliniowe. Na boku 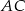 wybrano punkt
wybrano punkt 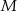 tak, że
tak, że 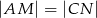 . Wykaż, że
. Wykaż, że 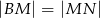 .
.
Rozwiązanie
Sposób I
Niech 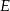 będzie takim punktem odcinka
będzie takim punktem odcinka 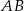 , że
, że 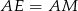 .
.
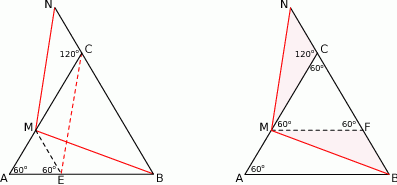
Trójkąt 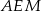 jest więc równoboczny, zatem
jest więc równoboczny, zatem 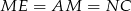 . Ponadto
. Ponadto
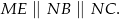
To oznacza, że czworokąt 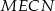 jest równoległobokiem. Zatem
jest równoległobokiem. Zatem 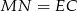 . Teraz wystarczy zauważyć, że przekątne trapezu równoramiennego
. Teraz wystarczy zauważyć, że przekątne trapezu równoramiennego 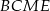 mają równe długości, czyli
mają równe długości, czyli
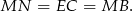
Sposób II
Niech 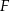 będzie takim punktem boku
będzie takim punktem boku 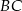 , że
, że 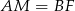 . Wtedy trójkąt
. Wtedy trójkąt 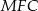 jest równoboczny, więc
jest równoboczny, więc 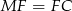 . Ponadto
. Ponadto
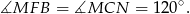
To oznacza, że trójkąty 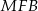 i
i 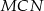 są przystające (mają dwa takie same boki i kąt między tymi bokami). W takim razie
są przystające (mają dwa takie same boki i kąt między tymi bokami). W takim razie 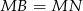 .
.
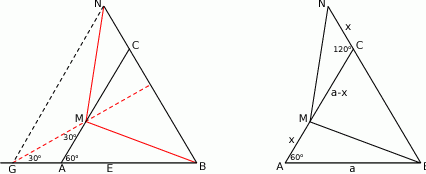
Sposób III
Niech 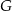 będzie takim punktem na przedłużeniu boku
będzie takim punktem na przedłużeniu boku 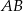 , że
, że 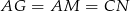 .
.
Trójkąt 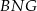 jest równoboczny (bo
jest równoboczny (bo 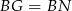 i
i 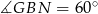 ), a trójkąt
), a trójkąt 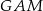 równoramienny. W takim razie
równoramienny. W takim razie
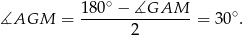
To oznacza, że prosta 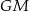 jest wysokością w trójkącie równobocznym
jest wysokością w trójkącie równobocznym 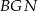 . Jest to więc też symetralna odcinka
. Jest to więc też symetralna odcinka 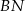 . Zatem
. Zatem 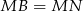 .
.
Sposób IV
Oznaczmy 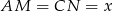 oraz
oraz 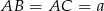 . Widać, że przy tych oznaczeniach łatwo obliczyć długości odcinków
. Widać, że przy tych oznaczeniach łatwo obliczyć długości odcinków 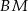 i
i 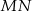 korzystając z twierdzenia cosinusów.
korzystając z twierdzenia cosinusów.
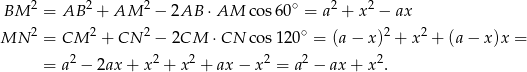
Widać zatem, że rzeczywiście 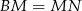 .
.

