Zadanie nr 5670373
Przez środek okręgu wpisanego w trójkąt równoboczny 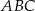 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 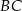 i przecinającą bok
i przecinającą bok 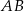 w punkcie
w punkcie 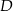 . Oblicz iloraz
. Oblicz iloraz 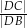 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
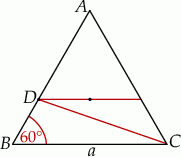
Oznaczmy długość boku trójkąta równobocznego przez  . Wiemy, że środek trójkąta równobocznego dzieli wysokość w stosunku
. Wiemy, że środek trójkąta równobocznego dzieli wysokość w stosunku 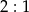 , czyli
, czyli
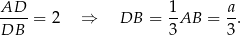
Możemy teraz z twierdzenia cosinusów wyliczyć długość odcinka 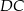 . Liczymy
. Liczymy
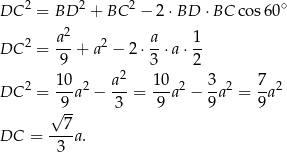
Zatem
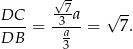
Odpowiedź: