Zadanie nr 1788680
W trójkącie równobocznym 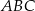 obrano na boku
obrano na boku 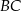 taki punkt
taki punkt 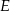 , że
, że 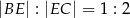 . Oblicz tangens kąta
. Oblicz tangens kąta 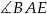 .
.
Rozwiązanie
Zacznijmy od rysunku i oznaczmy bok trójkąta przez  .
.
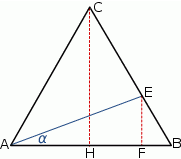
Sposob I
Obliczmy najpierw długość odcinka 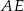 (z twierdzenia cosinusów).
(z twierdzenia cosinusów).
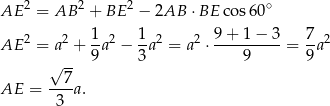
Stosując teraz twierdzenie sinusów w trójkącie 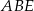 mamy
mamy
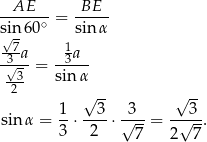
Cosinus możemy obliczyć z jedynki trygonometrycznej.
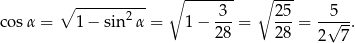
Zatem szukany tangens wynosi
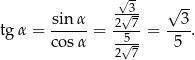
Sposób II
Zauważmy, że 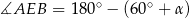 , więc stosując wzór na sinus sumy mamy
, więc stosując wzór na sinus sumy mamy
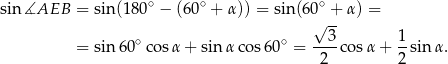
Stosujemy teraz twierdzenie sinusów w trójkącie 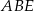 .
.
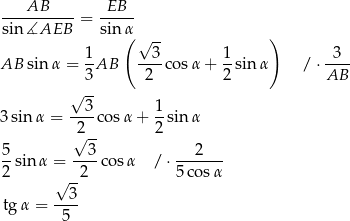
Sposob III
Zadanie ma znacznie prostsze rozwiązanie, jeżeli wykorzystamy odrobinę więcej geometrii. Dorysujmy wysokość 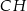 oraz równoległy do niej odcinek
oraz równoległy do niej odcinek 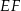 . Szukany tangens możemy obliczyć z trójkąta prostokątnego
. Szukany tangens możemy obliczyć z trójkąta prostokątnego 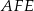 , aby jednak móc to zrobić musimy najpierw obliczyć długości odcinków
, aby jednak móc to zrobić musimy najpierw obliczyć długości odcinków 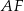 i
i 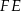 . Trójkąty
. Trójkąty 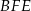 i
i 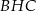 są podobne oraz znamy ich skalę podobieństwa
są podobne oraz znamy ich skalę podobieństwa
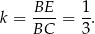
Mamy stąd
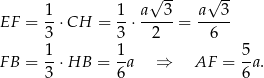
Mamy stąd
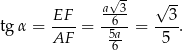
Odpowiedź: