/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoboczny/Kąty

Zadanie nr 9446233

Dodaj do ulubionych
Dodaj do rozwiązanych

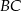Na boku BC trójkąta równobocznego 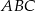ABC obrano taki punkt 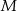M , że pole trójkąta 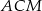ACM jest cztery razy mniejsze od pola trójkąta 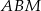ABM . Oblicz sinusy kątów 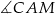∡CAM i ∡MAB .

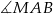Rozwiązanie

Zaczynamy od rysunku.

PIC

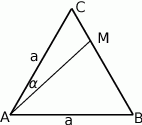
Oznaczmy jeden z szukanych kątów 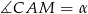∡CAM = α i policzmy pola obu trójkątów ze wzoru z sinusem.

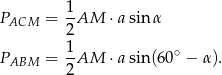
P = 1AM ⋅asin α ACM 2 1 ∘ PABM = -AM ⋅asin(60 − α ). 2

Stąd

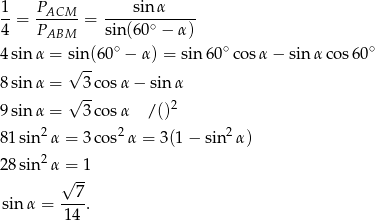
1- PACM-- ---sin-α----- 4 = P = sin (60∘ − α) ABM ∘ ∘ ∘ 4 sin α = sin-(60 − α) = sin6 0 cos α− sin α cos6 0 8 sin α = √ 3cos α− sin α √ -- 9 sin α = 3cos α / ()2 2 2 2 81 sin α = 3cos α = 3(1 − sin α) 28 sin2α = 1 √ -- --7- sin α = 14 .

Pozostało policzyć sinus drugiego z kątów. Z pierwszej równości w powyższych przekształceniach mamy

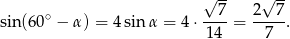
√ -- √ -- sin(60∘ − α) = 4sinα = 4⋅ --7-= 2--7. 14 7

 
Odpowiedź: 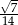√ - -174 i √ - 27-7

Wersja PDF