Zadanie nr 5183581
Wykaż, że jeżeli kąty trójkąta: 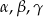 spełniają równanie
spełniają równanie 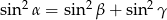 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Rozwiązanie
Szkicujemy trójkąt.
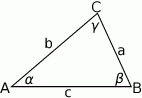
Zauważmy, że na mocy twierdzenia sinusów mamy
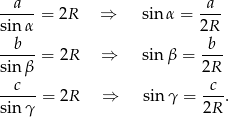
Zatem podany w treści warunek możemy zapisać w postaci
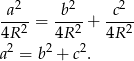
Zatem trójkąt jest prostokątny.

