Zadanie nr 5616926
- Uzasadnij, że jeśli długości boków trójkąta są równe
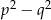 ,
, 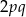 i
i 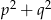 , gdzie
, gdzie 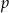 i
i 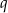 są liczbami dodatnimi takimi, że
są liczbami dodatnimi takimi, że 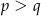 , to trójkąt ten jest prostokątny.
, to trójkąt ten jest prostokątny. - Wyznacz wszystkie naturalne wartości
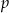 i
i 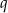 , dla których najkrótszy bok otrzymanego trójkąta ma długość 13.
, dla których najkrótszy bok otrzymanego trójkąta ma długość 13.
Rozwiązanie
- Musimy sprawdzić, czy suma kwadratów dwóch z podanych liczb jest równa kwadratowi trzeciej. Nietrudno zgadnąć, że największą z tych liczb jest
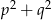 , musimy więc uzasadnić, że
, musimy więc uzasadnić, że 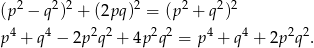
Otrzymana równość jest oczywiście zawsze prawdziwa, co kończy dowód.
- Ponieważ nie widać specjalnie, która z liczb
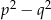 czy
czy 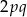 jest mniejsza, powinniśmy rozważyć dwa przypadki. Jednak
jest mniejsza, powinniśmy rozważyć dwa przypadki. Jednak 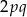 jest zawsze liczbą parzystą, nie może więc być równe 13. Zatem mamy równość
jest zawsze liczbą parzystą, nie może więc być równe 13. Zatem mamy równość 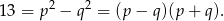
Ponieważ 13 jest liczbą pierwszą i liczby w obu nawiasach są liczbami naturalnymi, musimy mieć
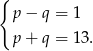
Dodając te równania stronami mamy
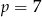 , czyli
, czyli 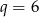 oraz pozostałe boki trójkąta są równe odpowiednio
oraz pozostałe boki trójkąta są równe odpowiednio 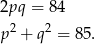
Odpowiedź: 84 i 85

