Zadanie nr 1551878
Na bokach trójkąta 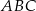 zbudowano kwadraty
zbudowano kwadraty 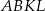 ,
, 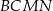 i
i  (zobacz rysunek).
(zobacz rysunek).
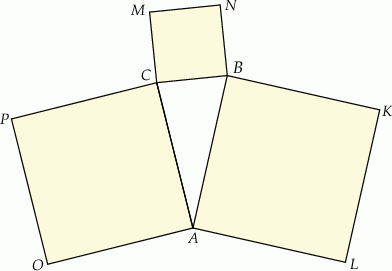
Kąty 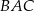 i
i 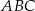 są ostre oraz suma ich tangensów jest równa
są ostre oraz suma ich tangensów jest równa  . Wykaż, że jeżeli pole kwadratu
. Wykaż, że jeżeli pole kwadratu 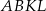 jest pięć razy większe od pola trójkąta
jest pięć razy większe od pola trójkąta 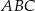 , to suma pól kwadratów
, to suma pól kwadratów 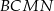 i
i 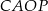 też jest pięć razy większa od pola trójkąta
też jest pięć razy większa od pola trójkąta  .
.
Rozwiązanie
Zastanówmy się przez chwilę co mamy udowodnić. Mamy pokazać, że
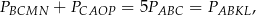
czyli, że
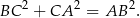
Mówiąc jeszcze inaczej, musimy wykazać, że trójkąt  jest prostokątny i
jest prostokątny i 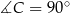 .
.
Teraz zajmijmy się podanymi założeniami. Przyjmijmy oznaczenia z poniższego rysunku.
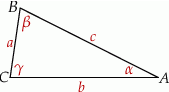
Mamy zatem
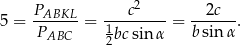
Możemy tę równość całkowicie zapisać w języku kątów trójkąta 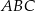 – wystarczy, że skorzystamy z twierdzenia sinusów.
– wystarczy, że skorzystamy z twierdzenia sinusów.
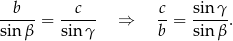
Mamy zatem
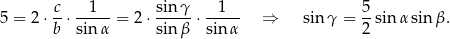
Na razie nie widać co możemy dalej z tym zrobić, więc popatrzmy na podaną informację o sumie tangensów kątów  i
i 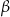 .
.
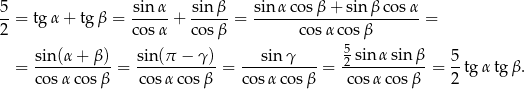
Stąd
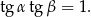
Pozostało wywnioskować z tej równości, że 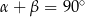 . Zrobimy to na dwa sposoby.
. Zrobimy to na dwa sposoby.
Sposób I
Wiemy, że
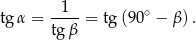
Po obu stronach tej równości mamy jednak kąty ostre, dla których tangens jest różnowartościowy. Zatem
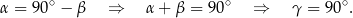
Sposób II
Podnieśmy równość
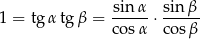
stronami do kwadratu.
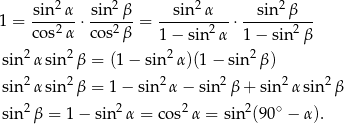
Ponieważ po obu stronach mamy kąty ostre, mamy stąd