/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Pole

Zadanie nr 4502334

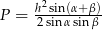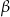Uzasadnij wzór na pole trójkąta h2sin(α+β)- P = 2sin αsin β , gdzie α i β są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość h .

Wersja PDF

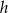Rozwiązanie

Zaczynamy od rysunku.

PIC

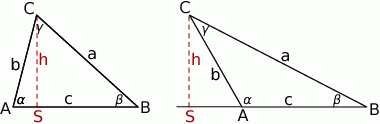
Sposób I

Pole jest oczywiście równe 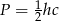P = 12 hc . Na mocy twierdzenia sinusów mamy

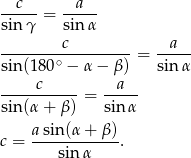
c a ----- = ----- sinγ sin α --------c--------- --a-- sin(180∘ − α − β ) = sin α c a -----------= ----- sin(α + β) sinα a-sin-(α+--β) c = sin α .

Jeżeli jeszcze raz popatrzymy na rysunek, to widać, że

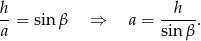
h- --h-- a = sinβ ⇒ a = sin β.

Zatem

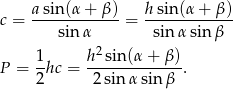
a sin (α+ β) hsin(α + β ) c = ----sinα---- = -sinα-sinβ-- 1- h2sin(α-+-β-) P = 2hc = 2sin αsin β .

Sposób II

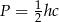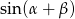Jak poprzednio punktem wyjścia jest wzór P = 1hc 2 . Przekształćmy najpierw podany w treści wzór (rozpiszemy sin(α + β ) ).

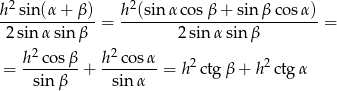
h2 sin (α+ β) h2(sin α cosβ + sin β cosα) ------------- = ---------------------------= 2sin αsin β 2 sinα sin β h2-cosβ- h2-cosα- 2 2 = sin β + sin α = h ctg β + h ctg α

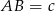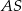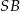Teraz pozostało zauważyć, że ta równość to "mniej więcej" rozkład odcinka AB = c na odcinki AS i SB . "mniej więcej", bo musimy osobno rozważyć przypadek trójkąta rozwartokątnego.

Najpierw jednak zauważmy, że dla trójkąta ostrokątnego (lub prostokątnego), mamy

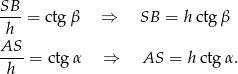
SB- h = ctgβ ⇒ SB = h ctg β AS ----= ctg α ⇒ AS = hctg α. h

Zatem otrzymana równość to dokładnie wzór 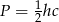1 P = 2hc .

Jezeli natomiast trójkąt jest rozwartokątny, to mamy

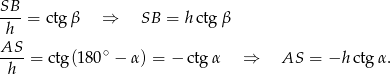
SB --- = ctg β ⇒ SB = hctg β h AS--= ctg(180∘ − α) = − ctgα ⇒ AS = −h ctg α. h

No i wszystko się zgadza, bo tym razem 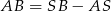AB = SB − AS .

Wersja PDF