/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Kąty

Zadanie nr 1435064

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli 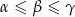α ≤ β ≤ γ są kątami wewnętrznymi trójkąta rozwartokątnego, to

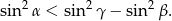
sin2 α < sin2γ − sin2 β.

Rozwiązanie

Szkicujemy trójkąt.

PIC

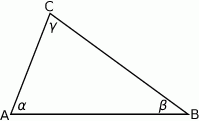
Korzystając z twierdzenia sinusów

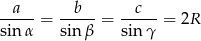
--a-- = -b---= --c-- = 2R sin α sin β sinγ

możemy zamienić nierówność, którą mamy udowodnić na nierówność równoważną.

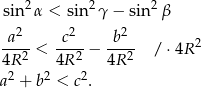
sin 2α < sin2 γ− sin 2β 2 2 2 -a-- < -c--− -b-- / ⋅4R 2 4R 2 4R 2 4R 2 a2 + b2 < c2.

Zauważmy teraz, że rozwartokątność trójkąta oznacza, że 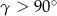γ > 90∘ , czyli 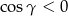cosγ < 0 . Na mocy twierdzenia cosinusów

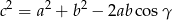
2 2 2 c = a + b − 2ab cosγ

mamy więc

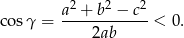
2 2 2 co sγ = a-+--b-−--c-< 0. 2ab

Licznik powyższego ułamka musi być ujemny, więc rzeczywiście

a2 + b2 < c2.
Wersja PDF