/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Kąty

Zadanie nr 1502514

Dodaj do ulubionych
Dodaj do rozwiązanych

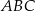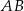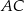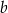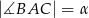W trójkącie ostrokątnym ABC bok AB ma długość c , długość boku AC jest równa b oraz |∡BAC | = α . Dwusieczna kąta 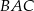BAC przecina bok 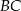BC trójkąta w punkcie 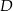D i odcinek 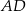AD ma długość 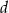d . Wykaż, że

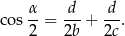
α- -d- d-- co s2 = 2b + 2c.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

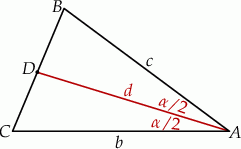
Sposób I

Korzystamy ze wzoru na pole trójkąta z sinusem.

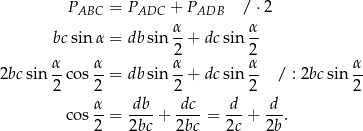
PABC = PADC + PADB / ⋅2 α- α- bc sin α = dbsin 2 + dc sin 2 α- α- α- α- α- 2bc sin 2 cos 2 = dbsin 2 + dc sin 2 / : 2bc sin 2 α db dc d d cos --= ----+ ----= ---+ ---. 2 2bc 2bc 2c 2b

Sposób II

Tym razem skorzystamy z twierdzenia o dwusiecznej

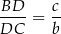
BD-- c- DC = b

oraz twierdzenia cosinusów

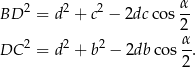
2 2 2 α- BD = d + c − 2dcco s2 α DC 2 = d2 + b2 − 2db cos--. 2

Mamy zatem

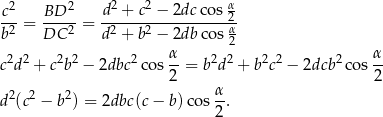
c2 BD 2 d2 + c2 − 2dc cos α -2-= ----2 = -2----2----------2α- b DC d + b − 2db cos 2 2 2 2 2 2 α- 2 2 2 2 2 α- cd + c b − 2dbc cos 2 = b d + b c − 2dcb cos 2 2 2 2 α- d (c − b ) = 2dbc(c− b)co s2 .

Jeżeli 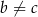b ⁄= c to dzielimy obie strony przez 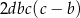2dbc(c − b) i mamy

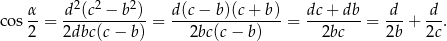
α- d2(c2-−-b2)- d(c−--b)(c+--b) dc-+-db- -d- d-- cos 2 = 2dbc(c − b) = 2bc(c − b) = 2bc = 2b + 2c.

Jeżeli natomiast 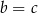b = c to trójkąt jest równoramienny i 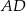AD jest jego wysokością. Wtedy

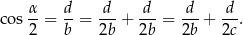
co s α-= d-= d--+ -d-= -d-+ d-. 2 b 2b 2b 2b 2c

Zauważmy, że obu rozwiązaniach nie miało znaczenia to, że trójkąt jest ostrokątny.

Wersja PDF