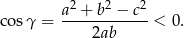Zadanie nr 3798789

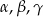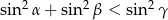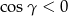Wykaż, że jeżeli α,β ,γ są kątami wewnętrznymi trójkąta i 2 2 2 sin α+ sin β < sin γ , to cos γ < 0 .

Rozwiązanie

Szkicujemy trójkąt.

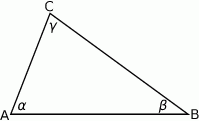
Korzystając z twierdzenia sinusów

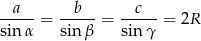
--a-- = -b---= --c-- = 2R sin α sin β sinγ

możemy zamienić sinusy w danej nierówności na długości boków trójkąta.

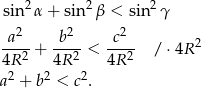
sin 2α + sin2β < sin 2γ 2 2 2 -a-- + -b-- < -c-- / ⋅4R 2 4R 2 4R 2 4R 2 a2 + b2 < c2.

Teraz korzystając z twierdzenia cosinusów

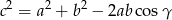
2 2 2 c = a + b − 2ab cosγ

obliczamy cos γ

a2 + b2 − c2 co sγ = ------------< 0. 2ab

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz