/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Kąty

Zadanie nr 4472470

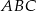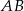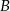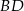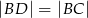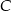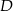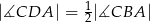W trójkącie ABC przedłużono bok AB poza wierzchołek B i odłożono odcinek BD taki, że |BD | = |BC | . Następnie połączono punkty C i D (rysunek). Wykaż, że |∡CDA | = 12|∡CBA | .

PIC

Wersja PDF

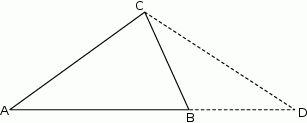
Rozwiązanie

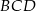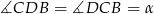Wiemy, że trójkąt BCD jest równoramienny, więc możemy oznaczyć kat ∡CDB = ∡DCB = α .

PIC

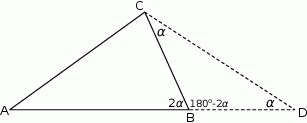
Wtedy

∘ ∘ ∡CBD = 180 − ∡CDB − ∡DCB = 180 − 2α ∡CBA = 180 ∘ − ∡CBD = 18 0∘ − (180∘ − 2α) = 2α = 2∡CDA .
Wersja PDF