/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Kąty

Zadanie nr 7368999

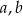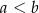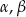Wykaż, że jeśli a,b są długościami boków trójkąta ostrokątnego takimi, że a < b oraz α ,β są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków 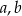a,b , to α < β .

Wersja PDF

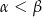Rozwiązanie

Zaczynamy od rysunku

PIC

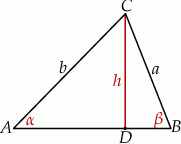
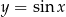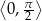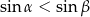Ponieważ funkcja y = sin x jest rosnąca w przedziale ⟨ ⟩ 0, π2- (w tym miejscu korzystamy z założenia, że trójkąt jest ostrokątny), wystarczy wykazać, że sin α < sin β .

Sposób I

Dorysujmy wysokość 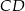CD . Mamy wtedy

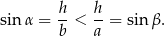
sin α = h-< h- = sinβ . b a

Sposób II

Korzystamy z twierdzenia sinusów.

2R sin α = a < b = 2R sin β / : 2R sin α < sin β.
Wersja PDF