Zadanie nr 9385995
W trójkącie ostrokątnym 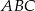 proste
proste 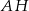 i
i 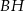 zawierają wysokości poprowadzone z wierzchołków
zawierają wysokości poprowadzone z wierzchołków 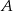 i
i 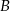 . Uzasadnij, że kąt
. Uzasadnij, że kąt 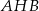 jest rozwarty.
jest rozwarty.
Rozwiązanie
Rozpoczynamy od rysunku.
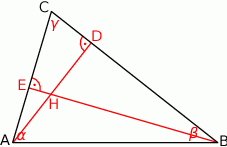
Sposób I
Suma kątów czworokąta 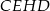 jest równa
jest równa 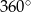 , więc
, więc
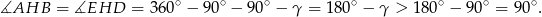
Ostatnia nierówność wynika z podanego założenia, że trójkąt 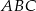 jest ostrokątny.
jest ostrokątny.
Sposób II
Z trójkątów prostokątnych 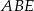 i
i 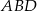 mamy
mamy
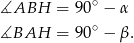
Obliczamy miarę kąta 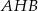 .
.