Zadanie nr 3934122
W trójkącie 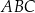 dwusieczna kąta
dwusieczna kąta 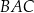 przecina bok
przecina bok 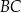 trójkąta w punkcie
trójkąta w punkcie 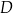 . Wykaż, że
. Wykaż, że
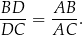
Rozwiązanie
Szkicujemy opisaną sytuację.

Sposób I
Trójkąty 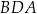 i
i 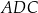 mają wspólną wysokość opuszczoną z wierzchołka
mają wspólną wysokość opuszczoną z wierzchołka 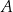 , więc stosunek ich pól jest równy stosunkowi ich podstaw. Zatem
, więc stosunek ich pól jest równy stosunkowi ich podstaw. Zatem
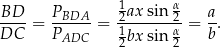
Sposób II
Tak samo jak w poprzednim sposobie zauważamy, że
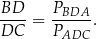
Teraz zauważmy jeszcze, że punkty dwusiecznej są jednakowo odległe od obu ramion kąta, więc odległości punktu 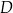 od boków
od boków 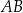 i
i 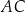 trójkąta są równe – oznaczmy tę odległość przez
trójkąta są równe – oznaczmy tę odległość przez 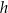 . Mamy zatem
. Mamy zatem
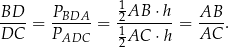
Sposób III
Tym razem skorzystamy z twierdzenia sinusów w trójkątach 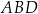 i
i 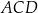 .
.
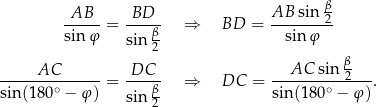
Ponieważ 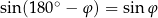 mamy stąd
mamy stąd
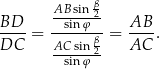
Sposób IV
Tym razem użyjemy odrobinę więcej geometrii. Niech 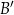 będzie takim punktem prostej
będzie takim punktem prostej 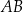 , że
, że 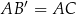 , a
, a 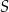 punktem wspólnym
punktem wspólnym 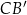 i dwusiecznej
i dwusiecznej 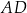 .
.
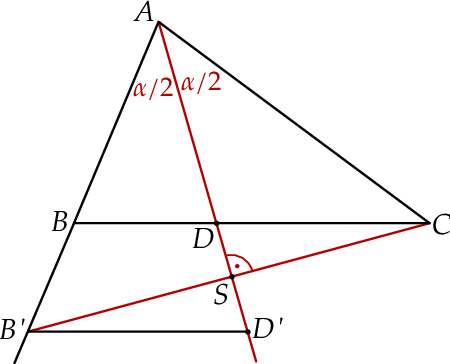
Trójkąt 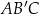 jest równoramienny, więc jego dwusieczna
jest równoramienny, więc jego dwusieczna 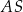 jest jednocześnie jego wysokością oraz symetralną boku
jest jednocześnie jego wysokością oraz symetralną boku 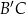 . W takim razie proste
. W takim razie proste 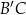 i
i 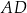 są prostopadłe oraz
są prostopadłe oraz 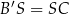 . Jeżeli teraz wybierzemy na dwusiecznej
. Jeżeli teraz wybierzemy na dwusiecznej 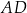 taki punkt
taki punkt 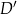 , że
, że 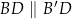 , to trójkąty
, to trójkąty 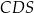 i
i 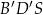 mają równe kąty oraz równe odpowiadające sobie przyprostokątne
mają równe kąty oraz równe odpowiadające sobie przyprostokątne 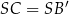 . Są więc przystające i
. Są więc przystające i 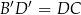 . Pozostało teraz skorzystać z podobieństwa trójkątów
. Pozostało teraz skorzystać z podobieństwa trójkątów 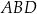 i
i 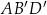 .
.
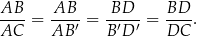
Równość, którą udowodniliśmy nosi nazwę twierdzenia o dwusiecznej.

