Zadanie nr 6229783
Odcinek 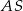 jest środkową trójkąta
jest środkową trójkąta 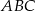 . Udowodnij, że
. Udowodnij, że 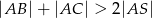 .
.
Rozwiązanie
Sposób I
Niech 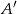 będzie obrazem punktu
będzie obrazem punktu 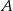 w symetrii względem punktu
w symetrii względem punktu 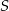 .
.
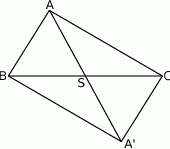
Otrzymany czworokąt 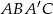 jest równoległobokiem (bo
jest równoległobokiem (bo 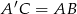 i
i 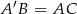 ), którego przekątne przecinają się w punkcie
), którego przekątne przecinają się w punkcie 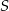 (bo
(bo 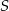 jest środkiem przekątnej
jest środkiem przekątnej 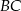 ). W takim razie
). W takim razie
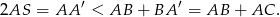
Sposób II
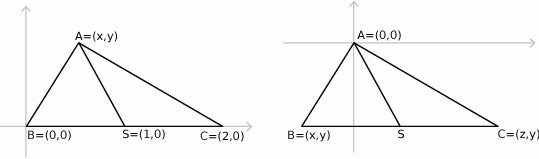
Umieśćmy trójkąt  w układzie współrzędnych. Ponieważ układ współrzędnych możemy wybrać dowolnie, możemy założyć, że
w układzie współrzędnych. Ponieważ układ współrzędnych możemy wybrać dowolnie, możemy założyć, że 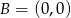 i
i 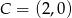 (umieszczamy układ na płaszczyźnie tak, aby: bok
(umieszczamy układ na płaszczyźnie tak, aby: bok 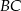 leżał na osi
leżał na osi 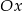 , punkt
, punkt 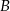 był w początku układu, oraz ustalamy jednostkę na osiach tak, aby
był w początku układu, oraz ustalamy jednostkę na osiach tak, aby 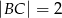 ). Mamy zatem
). Mamy zatem 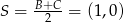 oraz
oraz 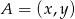 dla pewnych
dla pewnych 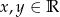 . Będziemy teraz przekształcać interesującą nas nierówność w sposób równoważny.
. Będziemy teraz przekształcać interesującą nas nierówność w sposób równoważny.
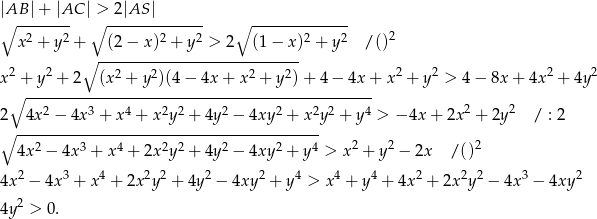
To jednak jest oczywiste, bo punkt 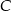 nie może leżeć na osi
nie może leżeć na osi 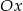 , więc
, więc 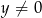 .
.
Sposób III
Tak jak poprzednio umieszczamy trójkąt 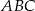 w układzie współrzędnych, ale tym razem umieśćmy układ tak, aby
w układzie współrzędnych, ale tym razem umieśćmy układ tak, aby 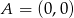 i aby bok
i aby bok 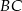 był równoległy do osi
był równoległy do osi 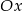 , czyli
, czyli 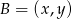 i
i 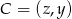 dla pewnych
dla pewnych 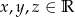 . Mamy więc
. Mamy więc 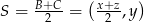 i tak jak poprzednio przekształcamy interesującą nas nierówność w sposób równoważny.
i tak jak poprzednio przekształcamy interesującą nas nierówność w sposób równoważny.
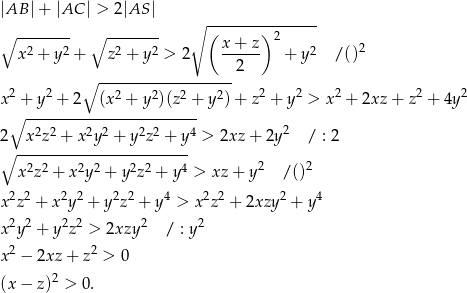
Otrzymana nierówność jest oczywiście spełniona, bo  . Po drodze dzieliliśmy przez
. Po drodze dzieliliśmy przez 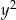 – mogliśmy to zrobić, bo punkt
– mogliśmy to zrobić, bo punkt  nie może leżeć na prostej
nie może leżeć na prostej 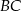 , wiec
, wiec 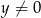 .
.
Powyższe rachunki mogły być jeszcze prostsze: wystarczyło założyć dodatkowo, że np. 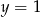 lub
lub 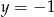 .
.

