Zadanie nr 6685079
Wykaż, że jeżeli w trójkącie dwusieczna pokrywa się ze środkową, to trójkąt ten jest równoramienny.
Rozwiązanie
Załóżmy, że dwusieczna i środkowa poprowadzone z wierzchołka 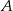 trójkąta
trójkąta 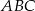 pokrywają się.
pokrywają się.
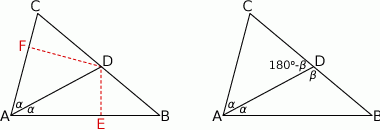
Sposób I
Niech 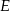 i
i 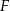 będą rzutami środka
będą rzutami środka 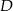 boku
boku 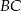 odpowiednio na proste
odpowiednio na proste 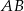 i
i 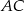 . Ponieważ punkt
. Ponieważ punkt 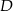 leży na dwusiecznej kąta
leży na dwusiecznej kąta 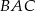 , to
, to 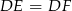 . Punkt
. Punkt 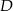 jest też środkiem odcinka
jest też środkiem odcinka 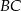 , więc
, więc 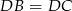 . To oznacza, że trójkąty prostokątne
. To oznacza, że trójkąty prostokątne 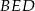 i
i 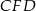 mają dwa boki tej samej długości (jedną z przyprostokątnych oraz przeciwprostokątną). W takim razie są przystające, skąd w szczególności otrzymujemy, że
mają dwa boki tej samej długości (jedną z przyprostokątnych oraz przeciwprostokątną). W takim razie są przystające, skąd w szczególności otrzymujemy, że 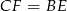 .
.
Zauważmy teraz, że trójkąty prostokątne 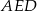 i
i 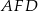 też są przystające (mają dwa boki tej samej długości). Mamy więc
też są przystające (mają dwa boki tej samej długości). Mamy więc
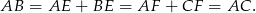
Sposób II
Tym razem napiszemy twierdzenie sinusów w trójkątach 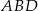 i
i 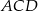 .
.
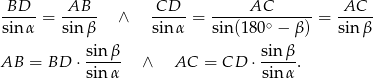
Ponieważ 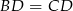 mamy stąd
mamy stąd 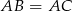 .
.
Sposób III
Tym razem załóżmy, że 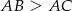 i niech
i niech 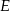 będzie takim punktem boku
będzie takim punktem boku 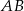 , że
, że 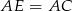 .
.
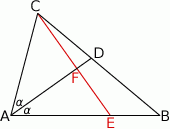
Trójkąt 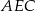 jest równoramienny i
jest równoramienny i 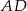 jest jego dwusieczną, więc
jest jego dwusieczną, więc 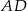 jest też jego wysokością i środkową, czyli
jest też jego wysokością i środkową, czyli 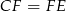 . To jednak oznacza, że
. To jednak oznacza, że 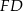 jest odcinkiem łączących środki boków trójkąta
jest odcinkiem łączących środki boków trójkąta 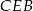 . Mamy stąd
. Mamy stąd
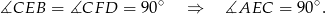
To jest jednak niemożliwe, bo kąt przy podstawie trójkąta równoramiennego nie może być prosty. Do tej sprzeczności doprowadziło nas założenie, że trójkąt 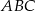 nie jest równoramienny.
nie jest równoramienny.
Sposób IV
Na mocy twierdzenia o dwusiecznej
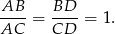
Zatem rzeczywiście 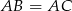 .
.

