Zadanie nr 7838876
Dwa boki trójkąta ostrokątnego wpisanego w okrąg o promieniu 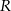 mają długości
mają długości 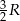 i
i 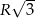 . Wykaż, że długość trzeciego boku wynosi
. Wykaż, że długość trzeciego boku wynosi 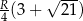 .
.
Rozwiązanie
Jak zwykle zaczynamy od rysunku.
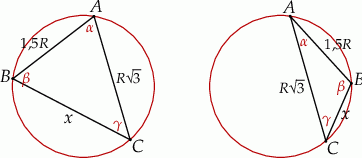
Robiąc go można zauważyć, że możliwe są dwie konfiguracje: gdy narysujemy już cięciwę długości 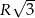 to cięciwę długości
to cięciwę długości 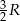 możemy narysować na dwa sposoby – po dwóch stronach pierwszej z cięciw. Przypadki te różnią się tym, że w jednym z nich zaznaczony kąt
możemy narysować na dwa sposoby – po dwóch stronach pierwszej z cięciw. Przypadki te różnią się tym, że w jednym z nich zaznaczony kąt 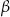 jest ostry, a w drugim rozwarty. Na szczęście z założenia interesuje nas tylko przypadek trójkąta ostrokątnego – to znacznie uprości rozwiązanie.
jest ostry, a w drugim rozwarty. Na szczęście z założenia interesuje nas tylko przypadek trójkąta ostrokątnego – to znacznie uprości rozwiązanie.
Sposób I
Długość trzeciego boku trójkąta obliczymy z twierdzenia sinusów, ale zanim to zrobimy, obliczmy funkcje trygonometryczne dwóch kątów trójkąta. Stosujemy twierdzenie sinusów.
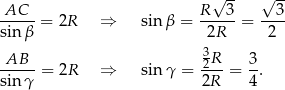
Ponieważ z założenia trójkąt jest ostrokątny, mamy stąd
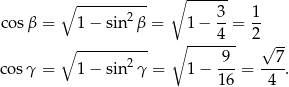
Możemy teraz obliczyć 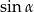 – korzystamy ze wzoru na sinus sumy.
– korzystamy ze wzoru na sinus sumy.
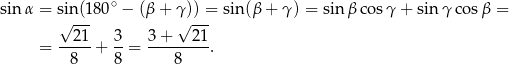
Stosujemy teraz twierdzenie sinusów.
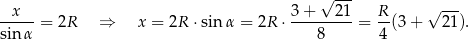
Sposób II
Tym razem będziemy łączyć ze sobą twierdzenia sinusów i cosinusów. Z twierdzenia sinusów mamy
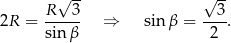
Ponieważ trójkąt jest ostrokątny, mamy stąd 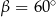 . Piszemy teraz twierdzenie cosinusów.
. Piszemy teraz twierdzenie cosinusów.
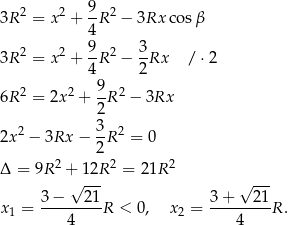
Ujemne rozwiązanie odrzucamy i mamy
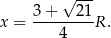
Sposób III
Pomysł jest taki, żeby obliczyć szukaną długość  trzeciego boku z twierdzenia cosinusów. Aby to zrobić, potrzebujemy znać
trzeciego boku z twierdzenia cosinusów. Aby to zrobić, potrzebujemy znać 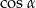 . Dokładnie tak samo jak I sposobie obliczamy wartości funkcji trygonometrycznych kątów
. Dokładnie tak samo jak I sposobie obliczamy wartości funkcji trygonometrycznych kątów 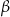 i
i 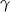 . To pozwala obliczyć
. To pozwala obliczyć 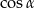 – korzystamy ze wzoru na cosinus sumy.
– korzystamy ze wzoru na cosinus sumy.
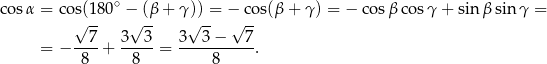
Stosujemy teraz twierdzenie cosinusów
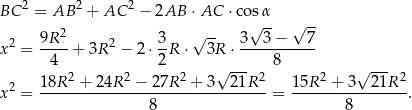
Aby zakończyć dowód wystarczy teraz zauważyć, że
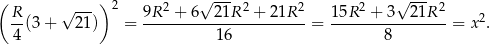
Sposób IV
Jak poprzednio chcemy obliczyć 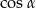 . Stosujemy twierdzenie sinusów (bo znamy promień okręgu opisanego).
. Stosujemy twierdzenie sinusów (bo znamy promień okręgu opisanego).
Liczymy
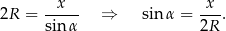
Teraz obliczymy 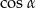 z jedynki trygonometrycznej – korzystamy z tego, że trójkąt jest ostrokątny.
z jedynki trygonometrycznej – korzystamy z tego, że trójkąt jest ostrokątny.
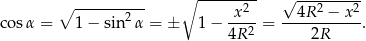
Stosujemy teraz twierdzenie cosinusów
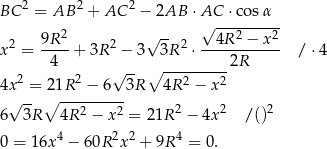
Podstawiamy 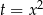 i dzielimy równanie stronami przez 4.
i dzielimy równanie stronami przez 4.
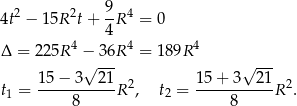
Zatem
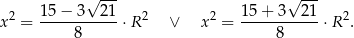
Łatwo sprawdzić, że w pierwszym przypadku 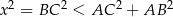 , czyli trójkąt jest rozwartokątny. Zatem
, czyli trójkąt jest rozwartokątny. Zatem
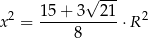
i tak samo jak w sposobie III uzasadniamy, że 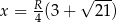 .
.
Sposób V
Tym razem, pomimo podobnego schematu, najpierw obliczymy 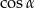 w zależności od
w zależności od 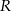 , a dopiero potem
, a dopiero potem  . Podobnie jak poprzednio piszemy twierdzenie cosinusów
. Podobnie jak poprzednio piszemy twierdzenie cosinusów
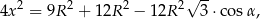
ale tym razem podstawiamy za 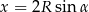 .
.
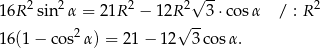
Podstawiamy 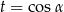 .
.
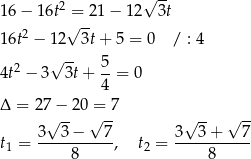
Wracając do twierdzenia cosinusów otrzymujemy
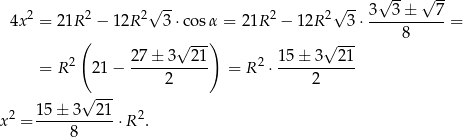
Teraz dokładnie tak samo jak w sposobie IV eliminujemy jedno rozwiązanie i dowodzimy, że 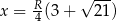 .
.

