Zadanie nr 7898952

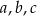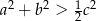Wykaż, że jeżeli a,b,c są długościami boków trójkąta to 2 2 1 2 a + b > 2c .

Rozwiązanie

Szkicujemy trójkąt.

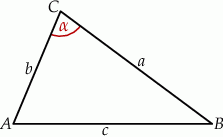
Sposób I

Zauważmy, że używając twierdzenia cosinusów możemy obliczyć 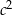w zależności od i 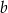. Dokładniej

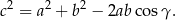
c2 = a2 + b2 − 2abco sγ .

Nierówność, którą mamy udowodnić przybiera więc postać

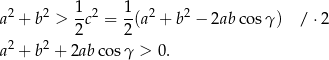
2 2 1-2 1- 2 2 a + b > 2c = 2 (a + b − 2ab cos γ) / ⋅ 2 a2 + b2 + 2ab cosγ > 0.

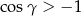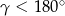Aby udowodnić tę nierówność korzystamy z tego, że cos γ > − 1 (bo γ < 180∘ ). Mamy zatem

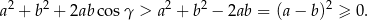
a2 + b 2 + 2ab cos γ > a2 + b2 − 2ab = (a− b )2 ≥ 0.

Sposób II

Tym razem za punkt wyjścia przyjmijmy nierówność trójkąta.

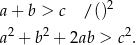
a+ b > c /()2 a2 + b 2 + 2ab > c2.

Aby przekształcić tę nierówność dalej zauważmy, że zawsze

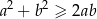
a2 + b2 ≥ 2ab

(nierówność ta jest równoważna nierówności 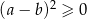(a− b)2 ≥ 0 ). W takim razie

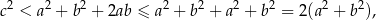
c2 < a2 + b2 + 2ab ≤ a 2 + b2 + a2 + b2 = 2(a2 + b2),

a to jest dokładnie nierówność, którą mieliśmy udowodnić.