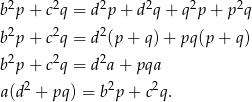Zadanie nr 8267023
W trójkącie 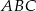 , o bokach długości
, o bokach długości 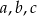 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 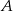 z punktem
z punktem 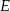 na boku
na boku 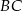 takim, że
takim, że 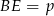 i
i 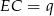 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 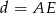 , to
, to 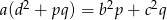 (twierdzenie Stewarta).
(twierdzenie Stewarta).
Rozwiązanie
Zaczynamy oczywiście od rysunku.
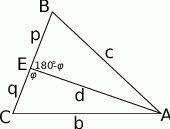
Z twierdzeń cosinusów w trójkątach 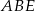 i
i 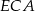 mamy
mamy
Aby pozbyć  mnożymy pierwsze równanie przez
mnożymy pierwsze równanie przez  , a drugie przez
, a drugie przez 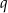 i dodajemy stronami.
i dodajemy stronami.