/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Długości odcinków

Zadanie nr 9893399

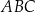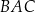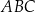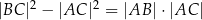W trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC . Wykaż, że prawdziwa jest równość |BC |2 − |AC |2 = |AB |⋅|AC | .

Wersja PDF

Rozwiązanie

Szkicujemy trójkąt.

PIC

Przy oznaczeniach rysunku, mamy udowodnić, że

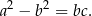
a2 − b 2 = bc.

Korzystając z twierdzenia sinusów mamy

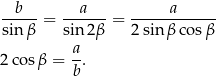
--b-- = --a---= -----a------ sin β sin 2β 2 sin β cosβ a- 2 cosβ = b.

Sposób I

Jeszcze raz korzystamy z twierdzenia sinusów.

b c c -----= --------∘------ = ------ sinβ sin(180 − 3 β) sin 3β csinβ = b sin 3β = b(sin β cos2β + sin 2β cosβ ) = 2 = b(sinβ (2co s β − 1) + 2sin β(cosβ cos β) )/ : sin β 2 2 2 c = b(2 cos β − 1 + 2 cos β ) = b 4co s β − 1 = (a 2 ) a2 = b ---− 1 = ---− b / ⋅b b 2 b bc = a2 − b2.

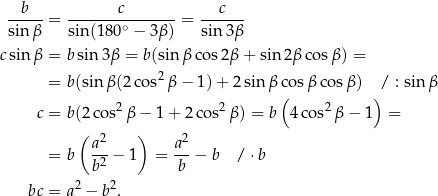
Sposób II

Piszemy twierdzenie cosinusów.

2 2 2 2 2 2 a--c b = a + c − 2ac cosβ = a + c − b a2c a2c 0 = a2 − b2 + c2 − ----= (a 2 − b2 − bc) + c2 + bc− ----= b b( ) = (a2 − b2 − bc) + c(bc + b2 − a2) = (a2 − b2 − bc) 1 − c- . b b

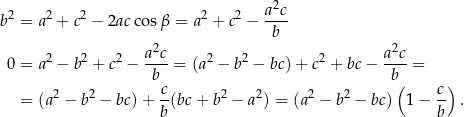
Jeżeli teraz 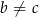b ⁄= c , to mamy tezę. Jeżeli natomiast 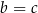b = c , to

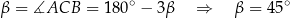
β = ∡ACB = 18 0∘ − 3β ⇒ β = 45∘

i trójkąt 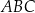ABC jest połówką kwadratu. Wtedy 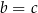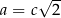b = c , √ -- a = c 2 i

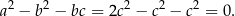
2 2 2 2 2 a − b − bc = 2c − c − c = 0 .

Sposób III

Tym razem dorysujmy dwusieczną 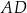AD i oznaczmy 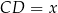CD = x . Trójkąt 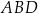ABD jest równoramienny, więc

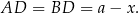
AD = BD = a− x.

Ponadto

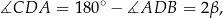
∡CDA = 180∘ − ∡ADB = 2β ,

więc trójkąt 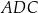ADC jest podobny do trójkąta 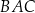BAC (mają takie same kąty). Stąd

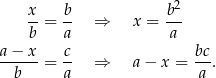
x b b2 --= -- ⇒ x = --- b a a a-−-x- c- bc- b = a ⇒ a − x = a .

Mamy zatem

bc b2 ---= a − x = a− --- / ⋅a a a bc = a2 − b2.
Wersja PDF