Zadanie nr 3187358
Odcinki 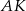 i
i 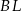 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 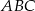 , a punkt
, a punkt 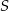 jest punktem ich przecięcia. Uzasadnij, że:
jest punktem ich przecięcia. Uzasadnij, że:
- na czworokącie
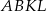 można opisać okrąg;
można opisać okrąg; - okręgi opisane na trójkątach
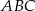 i
i 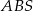 mają promienie równej długości.
mają promienie równej długości.
Rozwiązanie
Zaczynamy od rysunku.
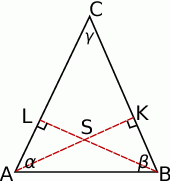
- Ponieważ kąty
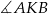 i
i 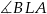 są proste, okrąg o średnicy
są proste, okrąg o średnicy 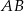 przechodzi przez punkty
przechodzi przez punkty 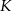 i
i 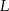 .
. - Oznaczmy standardowo miary kątów trójkąta (jak na obrazku). Z twierdzenia sinusów promień okręgu opisanego na trójkącie
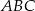 spełnia:
spełnia: 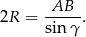
Aby porównać ten promień z promieniem okręgu opisanego na trójkącie
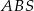 musimy wyliczyć kąt
musimy wyliczyć kąt 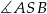 . Liczymy
. Liczymy 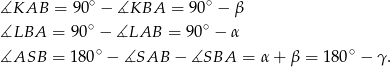
Kąt ten mogliśmy też wyliczyć trochę szybciej, patrząc na czworokąt
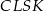 . Promień
. Promień 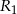 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 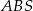 spełnia więc
spełnia więc