/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Różne

Zadanie nr 3995843

W trójkącie 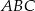ABC miara kąta 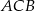ACB jest dwa razy większa od miary kąta 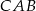CAB . Dwusieczna kąta 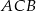ACB dzieli trójkąt 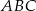ABC na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta ABC .

Wersja PDF

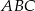Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

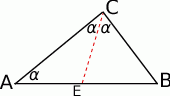
Skoro mamy udowodnić, że jeden z otrzymanych trójkątów ma takie same kąty jak trójkąt 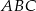ABC , obliczmy kąty tych trójkątów. Z trójkąta 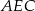AEC mamy

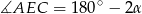
∡AEC = 180∘ − 2α

To nam daje

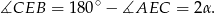
∡CEB = 180∘ − ∡AEC = 2α.

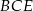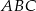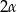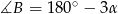No i wszystko jasne, trójkąt BCE ma takie same kąty jak trójkąt ABC , czyli α , 2α i ∡B = 180∘ − 3α .

Wersja PDF