Zadanie nr 4721167
W trójkącie 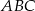 na boku
na boku 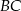 zaznaczono punkt
zaznaczono punkt 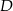 , na boku
, na boku 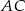 zaznaczono punkt
zaznaczono punkt 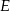 , na boku
, na boku 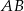 punkt
punkt 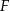 . Poprowadzono okręgi
. Poprowadzono okręgi 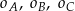 , w ten sposób, że do okręgu
, w ten sposób, że do okręgu 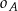 należą punkty
należą punkty 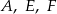 , do
, do 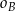 – punkty
– punkty 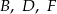 , a do
, a do 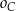 – punkty
– punkty 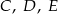 . Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
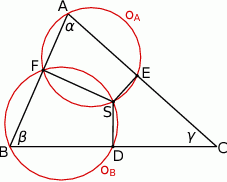
Zauważmy, że jeżeli 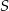 jest punktem wspólnym okręgów
jest punktem wspólnym okręgów 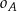 i
i 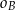 , to wystarczy udowodnić, że okrąg
, to wystarczy udowodnić, że okrąg 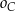 przechodzący przez punkty
przechodzący przez punkty 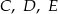 przechodzi też przez
przechodzi też przez 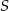 . Wystarczy zatem udowodnić, że na czworokącie
. Wystarczy zatem udowodnić, że na czworokącie 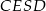 można opisać okrąg, czyli, że
można opisać okrąg, czyli, że 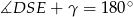 .
.
Aby to zrobić zauważmy, że na każdym z czworokątów 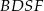 i
i 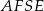 można opisać okrąg, więc
można opisać okrąg, więc
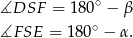
Zatem