/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij.../Różne

Zadanie nr 5888753

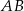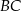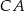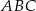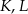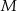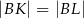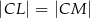Na bokach AB , BC i CA trójkąta ABC wybrano odpowiednio punkty K,L i M w ten sposób, że |BK | = |BL | i |CL | = |CM | . Okrąg opisany na trójkącie 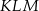KLM przecina bok 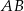AB tego trójkąta w punkcie 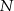N takim, że 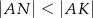|AN | < |AK | (zobacz rysunek).

PIC

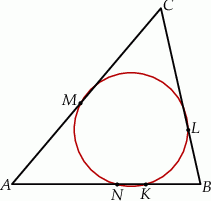
Udowodnij, że 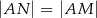|AN | = |AM | .

Wersja PDF

Rozwiązanie

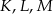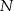Połączmy punkty K,L ,M i N oraz oznaczmy 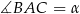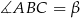∡BAC = α , ∡ABC = β i ∡ACB = γ .

PIC

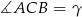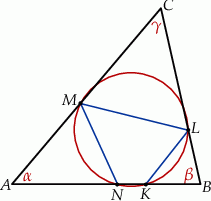
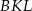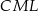Z założenia trójkąty BKL i CML są równoramienne, więc

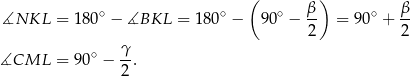
( ) ∡NKL = 180∘ − ∡BKL = 180∘ − 90∘ − β- = 9 0∘ + β- 2 2 ∘ γ- ∡CML = 90 − 2 .

Zauważmy teraz, ze czworokąt 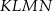KLMN jest wpisany w okrąg, więc

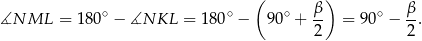
( ) ∘ ∘ ∘ β- ∘ β- ∡NML = 180 − ∡NKL = 180 − 90 + 2 = 90 − 2.

Mamy teraz wszystko, żeby obliczyć kąty trójkąta 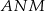ANM .

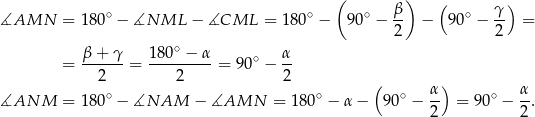
( ) ∘ ∘ ∘ β- ( ∘ γ-) ∡AMN = 180 − ∡NML − ∡CML = 180 − 90 − 2 − 90 − 2 = ∘ = β-+--γ = 180--−-α-= 90∘ − α- 2 2 2 ∘ ∘ ( ∘ α-) ∘ α- ∡ANM = 180 − ∡NAM − ∡AMN = 180 − α − 90 − 2 = 90 − 2.

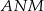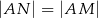To oznacza, że trójkąt ANM jest równoramienny, czyli rzeczywiście |AN | = |AM | .

Wersja PDF