Zadanie nr 7569624
W trójkącie 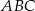 punkt
punkt 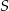 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 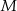 i
i 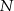 są punktami styczności tego okręgu z bokami
są punktami styczności tego okręgu z bokami 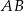 i
i 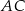 odpowiednio. Wykaż, że punkt
odpowiednio. Wykaż, że punkt 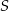 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 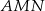 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
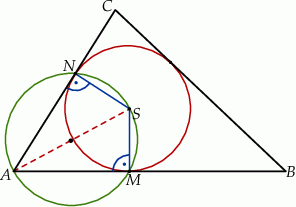
Odcinek łączący środek okręgu z punktem styczności jest prostopadły do stycznej poprowadzonej w tym punkcie, więc 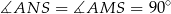 . To oznacza, że na czworokącie
. To oznacza, że na czworokącie 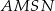 można opisać okrąg – jego średnicą jest zresztą odcinek
można opisać okrąg – jego średnicą jest zresztą odcinek 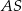 . Zatem rzeczywiście
. Zatem rzeczywiście 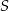 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 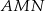 .
.

