Zadanie nr 8236307
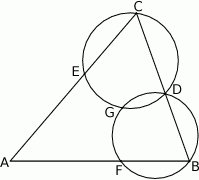
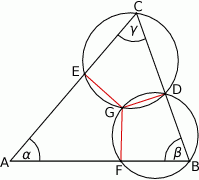
Okrąg 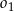 przechodzi przez wierzchołek
przechodzi przez wierzchołek 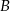 trójkąta
trójkąta 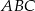 i przecina jego boki
i przecina jego boki 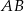 i
i 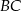 odpowiednio w punktach
odpowiednio w punktach 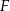 i
i 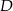 . Okrąg
. Okrąg 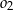 przechodzi przez wierzchołek
przechodzi przez wierzchołek 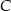 , przecina okrąg
, przecina okrąg 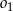 w punkcie
w punkcie 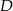 oraz w punkcie
oraz w punkcie 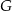 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 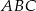 . Ponadto okrąg
. Ponadto okrąg 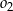 przecina bok
przecina bok 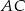 trójkąta w punkcie
trójkąta w punkcie 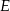 .
.
Udowodnij, że punkt 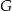 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 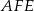 .
.
Rozwiązanie
Połączmy punkt 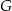 z punktami
z punktami 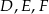 oraz oznaczmy miary kątów trójkąta tak jak na rysunku.
oraz oznaczmy miary kątów trójkąta tak jak na rysunku.
Musimy udowodnić, że na czworokącie 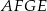 można opisać okrąg. Aby to zrobić wystarczy wykazać, że suma dwóch przeciwległych kątów czworokąta jest równa
można opisać okrąg. Aby to zrobić wystarczy wykazać, że suma dwóch przeciwległych kątów czworokąta jest równa 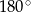 .
.
Czworokąty 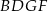 i
i 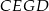 są wpisane w okrąg, więc
są wpisane w okrąg, więc
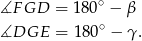
Mamy stąd
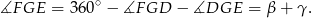
Zatem
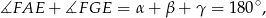
czyli rzeczywiście punkty 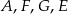 leżą na jednym okręgu.
leżą na jednym okręgu.

