Zadanie nr 1517931
W trójkącie 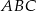 dane są
dane są 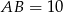 ,
, 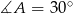 i
i 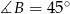 . Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
. Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku, tzn. niech 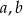 i
i  będą długościami boków naprzeciw wierzchołków
będą długościami boków naprzeciw wierzchołków 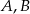 i
i 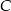 odpowiednio.
odpowiednio.
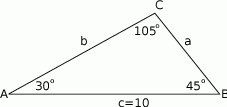
Ponieważ suma kątów w trójkącie wynosi 180 , więc
, więc 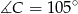 . Będziemy korzystać z twierdzenia sinusów, więc od razu wyliczmy sinusy tych kątów
. Będziemy korzystać z twierdzenia sinusów, więc od razu wyliczmy sinusy tych kątów
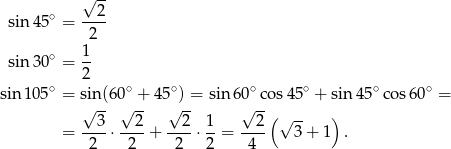
Teraz możemy już zastosować twierdzenie sinusów
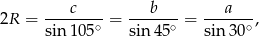
gdzie 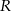 -promień okęgu opisanego na trójkącie. Uwzględniając wcześniejsze wyliczenia, oraz fakt, że
-promień okęgu opisanego na trójkącie. Uwzględniając wcześniejsze wyliczenia, oraz fakt, że 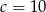 otrzymujemy:
otrzymujemy:
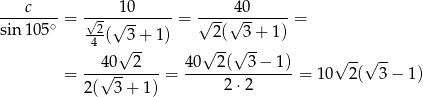
To pozwala łatwo wyliczyć szukane wielkości:
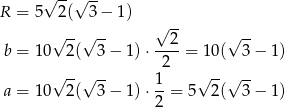
Odpowiedź: Boki: 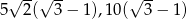 , promień:
, promień: 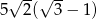 .
.

