Zadanie nr 2013143
Dany jest trójkąt 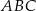 , w którym
, w którym 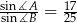 . Na boku
. Na boku 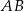 leży punkt
leży punkt 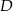 taki, że
taki, że 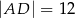 ,
, 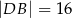 oraz
oraz 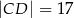 . Oblicz długość promienia okręgu opisanego na trójkącie
. Oblicz długość promienia okręgu opisanego na trójkącie  .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
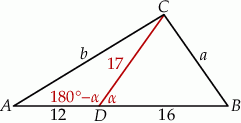
Zauważmy najpierw, że korzystając z twierdzenia sinusów możemy podany stosunek sinusów zamienić na stosunek długości boków  i
i  . Dokładniej,
. Dokładniej,
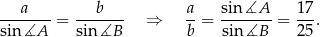
Żeby nie mieć ułamków, oznaczmy 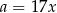 i
i 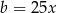 .
.
Oznaczmy 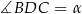 . Wtedy oczywiście
. Wtedy oczywiście 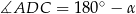 . Piszemy teraz twierdzenia cosinusów w trójkątach
. Piszemy teraz twierdzenia cosinusów w trójkątach 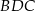 i
i 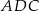 .
.
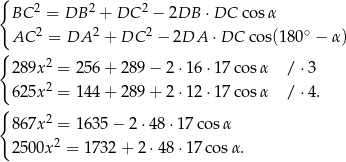
Dodajemy teraz równania układu stronami (żeby skrócić 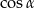 ).
).
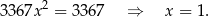
Zatem 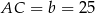 i
i 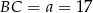 .
.
Promień okręgu opisanego obliczymy na kilka sposobów.
Sposób I
Ponieważ trójkąt 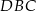 okazał się być równoramienny, łatwo jest obliczyć jego wysokość
okazał się być równoramienny, łatwo jest obliczyć jego wysokość 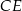 .
.
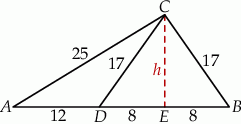
Z twierdzenia Pitagorasa mamy
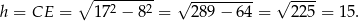
W takim razie
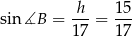
i na mocy twierdzenia sinusów mamy
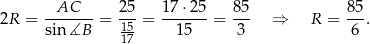
Sposób II
Tak jak w poprzednim sposobie obliczamy wysokość trójkąta 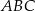 ,
, 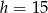 . W takim razie pole trójkąta
. W takim razie pole trójkąta 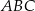 jest równe
jest równe
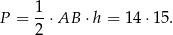
Korzystamy teraz ze wzoru 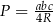 na pole trójkąta. Mamy zatem
na pole trójkąta. Mamy zatem
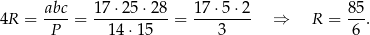
Sposób III
Pole trójkąta 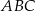 możemy obliczyć ze wzoru Herona
możemy obliczyć ze wzoru Herona
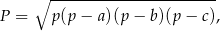
gdzie 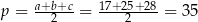 jest połową obwodu. Mamy zatem
jest połową obwodu. Mamy zatem
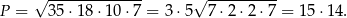
Korzystamy teraz ze wzoru 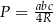 na pole trójkąta. Mamy zatem
na pole trójkąta. Mamy zatem
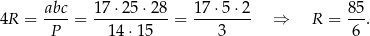
Sposób IV
Korzystając z twierdzenia cosinusów obliczamy 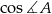 .
.
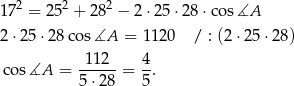
W takim razie
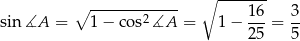
i na mocy twierdzenia sinusów mamy
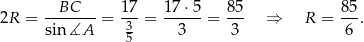
Odpowiedź: