/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów

Zadanie nr 2542420

Trójkąt ostrokątny, którego boki mają długości 17 i 16 ma pole równe 64. Oblicz promień okręgu opisanego na tym trójkącie.

Wersja PDF

Rozwiązanie

Szkicujemy trójkąt.

PIC

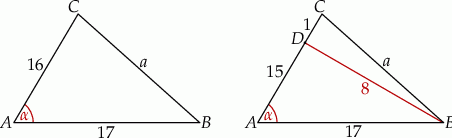
Promień okręgu opisanego na trójkącie możemy wyliczyć z twierdzenia sinusów, ale do tego potrzebujemy znać długość jednego z boków i sinus przeciwległego mu kąta.

Sposób I

Z podanego pola możemy obliczyć 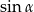sin α .

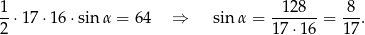
1-⋅17 ⋅16 ⋅sin α = 6 4 ⇒ sin α = --128--= -8-. 2 17 ⋅16 17

Długość boku 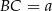BC = a obliczymy z twierdzenia cosinusów, więc obliczmy cosα .

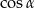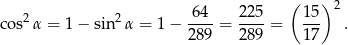
( ) 2 2 6-4- 225- 15- 2 cos α = 1 − sin α = 1− 289 = 289 = 17 .

Wiemy, że trójkąt jest ostrokątny, więc to oznacza, że 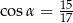cosα = 15 17 . Liczymy teraz długość boku BC .

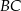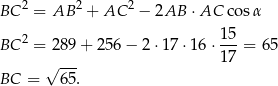
BC 2 = AB 2 + AC 2 − 2AB ⋅AC cos α 2 15- BC = 289 + 256 − 2 ⋅17 ⋅16 ⋅17 = 65 √ --- BC = 65.

Teraz łatwo obliczyć promień okręgu opisanego.

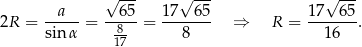
√ --- √ --- √ --- a 65 1 7 65 1 7 65 2R = ----- = --8-- = ------- ⇒ R = -------. sin α 17 8 16

Sposób II

Tym razem dorysujmy wysokość 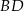BD (spodek wysokości jest na boku 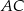AC , bo trójkąt jest ostrokątny). Z podanego pola mamy

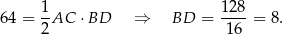
6 4 = 1-AC ⋅ BD ⇒ BD = 128-= 8. 2 1 6

Na mocy twierdzenia Pitagorasa w trójkącie 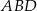ABD mamy

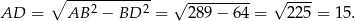
∘ ------------ √ --------- √ ---- AD = AB 2 − BD 2 = 28 9− 64 = 225 = 15.

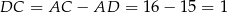Zatem DC = AC − AD = 16− 15 = 1 .

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 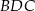BDC

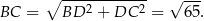
∘ ------------ √ --- BC = BD 2 + DC 2 = 65 .

Z trójkąta 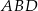ABD mamy

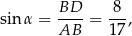
BD-- -8- sinα = AB = 17,

zatem na mocy twierdzenia sinusów

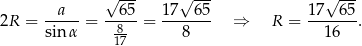
√ --- √ --- √ --- --a-- ---65 1-7--65 1-7--65 2R = sin α = 8- = 8 ⇒ R = 16 . 17

 
Odpowiedź: 17√ 65- --16-

Wersja PDF