/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów

Zadanie nr 3573514

Punkt 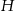H jest punktem wspólnym wysokości trójkąta ostrokątnego 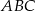ABC wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie ABH .

Wersja PDF

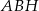Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

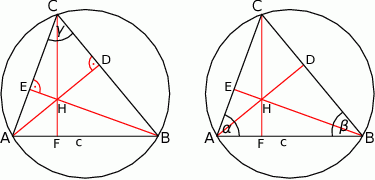
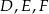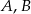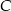Niech D ,E ,F będą spodkami wysokości opuszczonych odpowiednio z wierzchołków A ,B i C . Oznaczmy ponadto 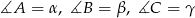∡A = α , ∡B = β, ∡C = γ oraz AB = c .

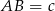Sposób I

Na mocy twierdzenia sinusów

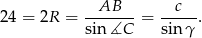
24 = 2R = --AB---= --c--. sin ∡C sinγ

Spróbujemy w podobny sposób obliczyć promień okręgu opisanego na trójkącie 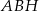ABH . Zauważmy, że (patrzymy na czworokąt CEHD )

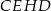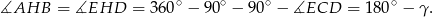
∡AHB = ∡EHD = 360∘ − 90∘ − 90 ∘ − ∡ECD = 18 0∘ − γ.

Zatem na mocy twierdzenia sinusów promień 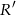′ R okręgu opisanego na trójkącie 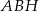ABH spełnia warunek.

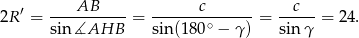
2R ′ = ----AB-----= -------c------ = --c-- = 24. sin ∡AHB sin(180 ∘ − γ ) sin γ

Zatem 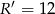R ′ = 12 .

Sposób II

Na mocy twierdzenia sinusów

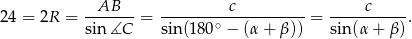
24 = 2R = --AB--- = ---------c----------= -----c-----. sin ∡C sin (180∘ − (α + β)) sin(α + β)

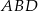Spróbujemy w podobny sposób obliczyć promień okręgu opisanego na trójkącie ABH . Zauważmy, że trójkąty ABE i ABD są prostokątne, co oznacza, że

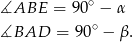
∡ABE = 90∘ − α ∘ ∡BAD = 90 − β.

Zatem (patrzymy na trójkąt 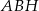ABH )

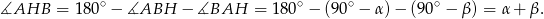
∡AHB = 180∘ − ∡ABH − ∡BAH = 180∘ − (90∘ − α) − (90∘ − β) = α + β .

Zatem na mocy twierdzenia sinusów promień 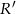R′ okręgu opisanego na trójkącie 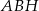ABH spełnia warunek.

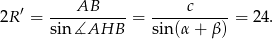
AB c 2R ′ = -----------= -----------= 24. sin∡AHB sin(α + β)

Zatem 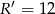′ R = 12 .  
Odpowiedź: 12

Wersja PDF