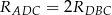/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów

Zadanie nr 3979315

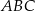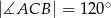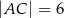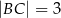W trójkącie ABC dane są kąt ∘ |∡ACB | = 12 0 , |AC | = 6 i |BC | = 3 . Dwusieczna kąta 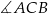∡ACB przecina bok 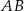AB w punkcie D .

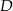  • Oblicz długość odcinka CD .
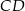  • Jaki jest związek miedzy długościami promieni: okręgu opisanego na trójkącie 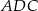ADC i okręgu opisanego na trójkącie 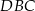DBC ? Odpowiedź uzasadnij.
Wersja PDF

Rozwiązanie

  •  

    Sposób I

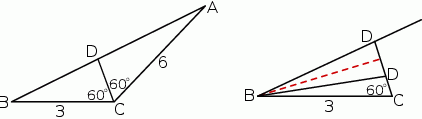
    Oznaczmy szukaną długość przez CD = x .

    PIC

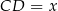    Policzymy pole trójkąta 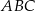ABC na dwa sposoby (korzystamy ze wzoru z sinusem).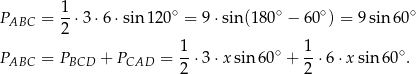

    1- ∘ ∘ ∘ ∘ PABC = 2 ⋅3 ⋅6 ⋅sin 120 = 9⋅sin(1 80 − 60 ) = 9 sin 60 1 1 PABC = PBCD + PCAD = --⋅3⋅x sin6 0∘ + --⋅6⋅x sin6 0∘. 2 2

    Mamy zatem

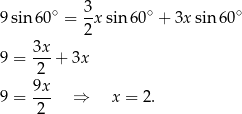
    3 9sin 60∘ = --xsin 60∘ + 3x sin 60∘ 2 9 = 3x-+ 3x 2 9x- 9 = 2 ⇒ x = 2.

    Sposób II

    Plan jest prosty: najpierw obliczymy długość boku 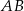AB , potem, z twierdzenia o dwusiecznej wyliczymy 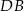DB . Na koniec, z twierdzenia cosinusów, wyliczymy CD .

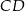    Bok 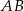AB wyliczymy z twierdzenia cosinusów w trójkącie ABC .

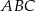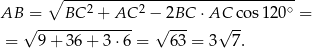
    ∘ -------------------------------- AB = BC 2 + AC 2 − 2BC ⋅AC cos120 ∘ = √ ------------- √ --- √ -- = 9 + 36 + 3 ⋅6 = 6 3 = 3 7.

    Na mocy twierdzenia o dwusiecznej,

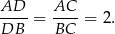
    AD-- AC-- DB = BC = 2.

    Zatem

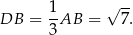
    √ -- DB = 1-AB = 7. 3

    Stosujemy teraz twierdzenie cosinusów do trójkąta DBC (oznaczmy DC = x ).

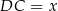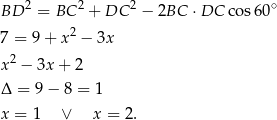
    2 2 2 ∘ BD = BC + DC − 2BC ⋅DC cos6 0 7 = 9+ x2 − 3x x 2 − 3x + 2 Δ = 9 − 8 = 1 x = 1 ∨ x = 2.

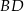    Spróbujmy się teraz zastanowić dlaczego wyszły dwie wartości x . Zauważmy, że przy ustalonych długościach odcinków BC i BD oraz kącie 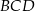BCD , są dwa możliwe położenia punktu 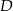D (symetryczne względem przerywanej linii). Jeden z tych punktów daje kąt rozwarty 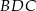BDC a drugi daje kąt ostry. W naszej sytuacji 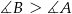∡B > ∡A , więc kąt 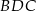BDC ma być ostry, czyli CD = x = 2 .

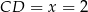    Inny sposób ustalenia, które rozwiązanie jest prawidłowe, to napisanie twierdzenia cosinusów w trójkącie CAD :

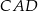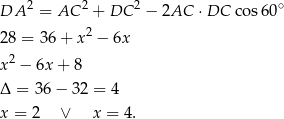
    2 2 2 ∘ DA = AC + DC − 2AC ⋅DC co s60 28 = 3 6+ x 2 − 6x 2 x − 6x + 8 Δ = 36− 32 = 4 x = 2 ∨ x = 4.

    Widać, że 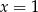x = 1 nie jest pierwiastkiem, a 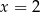x = 2 jest.  
    Odpowiedź: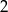 2

  • Jak zauważyliśmy w poprzednim podpunkcie, 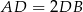AD = 2DB , więc na mocy twierdzenia sinusów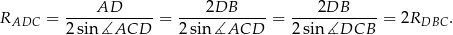
    RADC = -----AD----- = ----2DB----- = ---2DB------= 2RDBC . 2 sin∡ACD 2 sin ∡ACD 2sin∡DCB

     
    Odpowiedź: R = 2R ADC DBC

Wersja PDF