/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów

Zadanie nr 4744803

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie 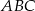ABC dane są długości boków: 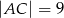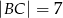|AC | = 9 , |BC | = 7 . Wiadomo też, że miara kąta 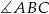∡ABC jest dwa razy większa od miary kąta 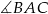∡BAC . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.

Rozwiązanie

Zaczynamy od rysunku.

PIC

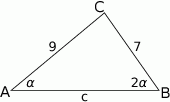
Podane dane aż się proszą, żeby napisać twierdzenie sinusów.

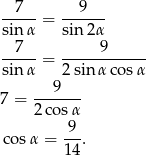
--7-- = ---9-- sinα sin 2α --7-- ------9----- sinα = 2 sinα cos α 9 7 = ------- 2 cos α co sα = 9-. 14

Możemy teraz napisać twierdzenie cosinusów tak aby wyliczyć długość c trzeciego boku.

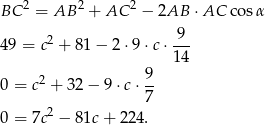
BC 2 = AB 2 + AC 2 − 2AB ⋅AC cos α 9 49 = c2 + 81 − 2 ⋅9⋅ c⋅--- 1 4 0 = c2 + 32 − 9 ⋅c⋅ 9- 7 0 = 7c2 − 81c + 224 .

Liczymy dalej

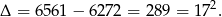
2 Δ = 6561 − 6272 = 289 = 17 .

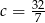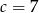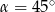Zatem 32 c = 7 lub c = 7 . Zauważmy, że druga wartość c oznacza, że trójkąt jest równoramienny i ∘ α = 45 , co nie zgadza się z wcześniej wyliczonym cosinusem. Zatem c = 327- .

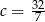Aby wyliczyć promień okręgu wpisanego skorzystamy ze wzoru na pole

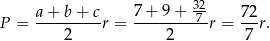
32 P = a-+-b-+-cr = 7+--9+--7-r = 7-2r. 2 2 7

Ponieważ chcemy wyliczyć iloraz 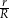r R- , fajnie byłoby mieć podobny wzór z R . Wyprowadźmy go zatem (korzystamy z twierdzenia sinusów)

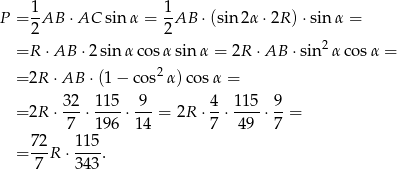
P = 1AB ⋅AC sinα = 1-AB ⋅(sin 2α ⋅2R )⋅sinα = 2 2 =R ⋅AB ⋅2sin αco sα sin α = 2R ⋅AB ⋅sin 2α cosα = 2 = 2R ⋅AB ⋅(1 − cos α)cos α = 3 2 115 9 4 115 9 = 2R ⋅---⋅ ----⋅---= 2R ⋅ -⋅ ----⋅--= 7 196 14 7 49 7 = 72-R ⋅ 115-. 7 343

Dzielimy teraz oba wzory na pole stronami i mamy

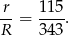
r 115 -- = ---. R 343

Jeżeli chodzi o alternatywne metody rozwiązania, to bok c można też wyliczyć z twierdzenia sinusów, trzeba tylko do tego obliczyć 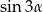sin3 α .  
Odpowiedź: 115 343

Wersja PDF