/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów

Zadanie nr 5515565

Dodaj do ulubionych
Dodaj do rozwiązanych

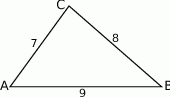
Dany jest trójkąt o bokach długości 7,8,9.

  • Oblicz promień okręgu wpisanego w ten trójkąt.
  • Oblicz sumę sinusów kątów tego trójkąta.

Rozwiązanie

Możemy naszkicować sobie taki trójkąt.

PIC

  • Skorzystamy ze wzoru na pole 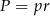P = pr , gdzie 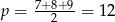p = 7+-8+-9 = 12 2 jest połową obwodu, a r jest długością promienia wpisanego. Mamy więc
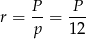
    P P r = --= --- p 12

    i pozostało wyliczyć pole trójkąta. Korzystamy ze wzoru Herona.

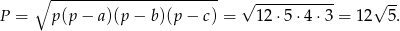
    ∘ ----------------------- √ ----------- √ -- P = p (p − a)(p− b)(p − c) = 12 ⋅5 ⋅4⋅ 3 = 12 5.

    Zatem

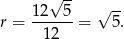
    √ -- 1-2--5 √ -- r = 12 = 5.

     
    Odpowiedź: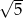 √ -- 5

  • Korzystamy ze wzoru na pole z sinusem.
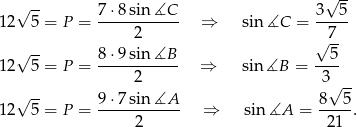
    √ -- √ -- 12 5 = P = 7⋅8-sin∡C-- ⇒ sin ∡C = 3---5 2 √ 7- √ -- 8⋅9 sin∡B 5 12 5 = P = ----------- ⇒ sin ∡B = ---- 2 3√ -- 12√ 5-= P = 9⋅7-sin∡A--- ⇒ sin ∡A = 8--5. 2 21

    Zatem suma jest równa

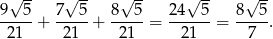
    √ -- √ -- √ -- √ -- √ -- 9--5-+ 7--5-+ 8--5-= 24--5-= 8--5-. 21 21 21 21 7

     
    Odpowiedź: √- 8-5- 7

Wersja PDF