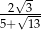/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów

Zadanie nr 8055110

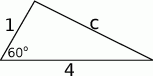
Długości dwóch boków trójkąta są równe 1 i 4, a miara kąta zawartego między nimi wynosi 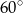6 0∘ .

  • Oblicz pole tego trójkąta.
  • Oblicz promień okręgu opisanego na tym trójkącie.
  • Oblicz promień okręgu wpisanego w ten trójkąt.
Wersja PDF

Rozwiązanie

PIC

  • Liczymy
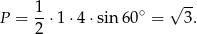
    1- ∘ √ -- P = 2 ⋅1 ⋅4⋅sin 60 = 3.

     
    Odpowiedź: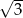 √ -- 3

  • Promień okręgu opisanego wyliczymy z twierdzenia sinusów, ale aby to zrobić wyliczmy najpierw długość trzeciego boku (z twierdzenia cosinusów).
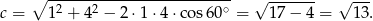
    ∘ -2----2-----------------∘ √ ------- √ --- c = 1 + 4 − 2 ⋅1 ⋅4⋅ cos60 = 17− 4 = 13.

    Zatem

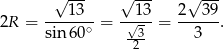
    √ 13- √ 13- 2√ 39- 2R = ------- = -√---= -----. sin 60∘ 23- 3

     
    Odpowiedź: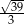 √-- -339-

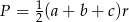  • Promień okręgu wpisanego obliczymy ze wzoru P = 1(a + b + c)r 2 .
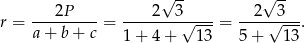
    √ -- √ -- ---2P---- ---2---3----- --2--3--- r = a + b + c = 1+ 4 + √ 1-3 = 5 + √ 13-.

     
    Odpowiedź: √- -2√3-- 5+ 13

Wersja PDF