/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Pole

Zadanie nr 2399890

Długość przeciwprostokątnej trójkąta prostokątnego o obwodzie 90 jest liczbą całkowitą i jest o 1 większa od długości jednej z przyprostokątnych. Oblicz pole tego trójkąta.

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy długość przeciwprostokątnej przez c to jedna z przyprostokątnych ma długość 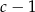c− 1 , a druga

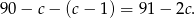
90− c− (c − 1) = 91− 2c.

PIC

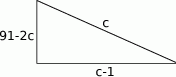
Zapisując twierdzenie Pitagorasa otrzymujemy równanie

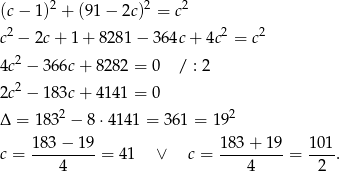
2 2 2 (c− 1 ) + (91 − 2c ) = c c2 − 2c + 1 + 82 81− 364c + 4c2 = c2 4c2 − 366c+ 8282 = 0 / : 2 2 2c − 183c+ 4141 = 0 Δ = 1832 − 8⋅4 141 = 361 = 192 c = 183-−-19-= 41 ∨ c = 183-+-19-= 101-. 4 4 2

Ponieważ przeciwprostokątna ma mieć długość całkowitą, odrzucamy drugie rozwiązanie. Zatem 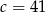c = 41 i przyprostokątne mają długości 9 i 40. Pole jest więc równe

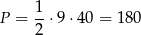
1- P = 2 ⋅9 ⋅40 = 18 0

 
Odpowiedź: 180

Wersja PDF