W trójkącie prostokątnym odległość punktu przecięcia się środkowych od wierzchołka kąta prostego wynosi 2 cm. Wysokość trójkąta poprowadzona na przeciwprostokątną ma długość 2,5 cm. Oblicz pole tego trójkąta.
Narysujmy najpierw opisaną sytuację.
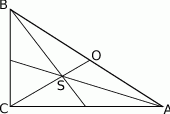
Ponieważ punkt przecięcia się środkowych dzieli każdą z nich w stosunku 2:1 (patrząc od wierzchołka), to możemy wyliczyć długość środkowej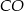 
.
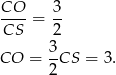
Pozostało teraz zauważyć, że ponieważ środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej, to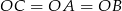 
, czyli 
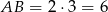. Możemy więc obliczyć szukane pole
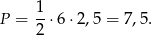
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
