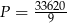/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Pole

Zadanie nr 6202631

Przyprostokątne trójkąta prostokątnego 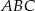ABC mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta 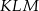KLM podobnego do trójkąta 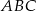ABC . Oblicz pole trójkąta KLM .

Wersja PDF

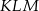Rozwiązanie

Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej trójkąta 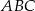ABC

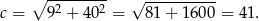
∘ --------- √ ---------- c = 92 + 402 = 81 + 160 0 = 41.

Najkrótszy bok trójkąta 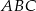ABC ma długość 9, więc skala podobieństwa trójkąta 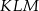KLM do trójkąta 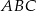ABC jest równa

k = 41. 9

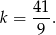
Teraz możemy łatwo policzyć długość drugiej przyprostokątnej trójkąta 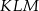KLM .

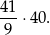
41-⋅40. 9

Pole trójkąta 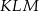KLM jest więc równe

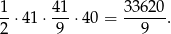
1-⋅41 ⋅ 4-1⋅ 40 = 33-620. 2 9 9

 
Odpowiedź: P = 336920-

Wersja PDF