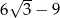/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Pole

Zadanie nr 9564937

W trójkącie prostokątnym 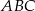ABC z wierzchołka kąta prostego poprowadzono odcinek 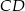CD taki, że 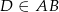D ∈ AB . Trójkąt 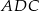ADC jest równoboczny. Oblicz pole trójkąta 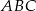ABC , wiedząc, że jego obwód jest równy 6.

Wersja PDF

Rozwiązanie

Naszkicujmy opisaną sytuację.

PIC

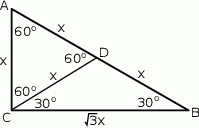
Sposób I

Jeżeli trójkąt 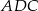ADC jest równoboczny, to 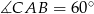∘ ∡CAB = 60 . Jeżeli oznaczymy teraz 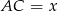AC = x , to

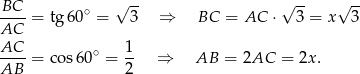
√ -- √ -- √ -- -BC- = tg 60∘ = 3 ⇒ BC = AC ⋅ 3 = x 3 AC AC-- ∘ 1- AB = co s60 = 2 ⇒ AB = 2AC = 2x .

Korzystamy teraz z podanego obwodu.

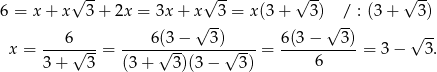
√ -- √ -- √ -- √ -- 6 = x + x 3+ 2x = 3x + x 3 = x(3 + 3 ) / : (3 + 3) √ -- √ -- x = ---6√---= ----6(√3−----3)√----= 6-(3−----3) = 3 − √ 3. 3 + 3 (3+ 3)(3− 3) 6

Pole trójkąta 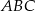ABC jest więc równe

√ -- √ -- √ -- P = 1-⋅AC ⋅BC = --3-⋅x2 = --3-(3− 3)2 = 2√ -- 2 √ -- 2 3 √ -- 3 √ -- √ -- √ -- √ -- = ----(9− 6 3+ 3) = ----(12− 6 3) = 3(6 − 3 3 ) = 6 3 − 9. 2 2

Sposób II

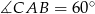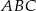Tak jak poprzednio zauważamy, że ∡CAB = 60∘ . To oznacza, że ∡ABC = 30 ∘ i trójkąt ABC jest połówką trójkąta równobocznego. Jeżeli więc oznaczymy 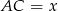AC = x , to

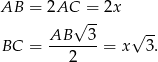
AB = 2AC√ =-2x AB 3 √ -- BC = -------= x 3. 2

Wartość x oraz pole obliczamy tak samo jak w poprzednim sposobie.

Sposób III

Oznaczmy 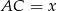AC = x . Trójkąt 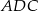ADC jest równoboczny, więc 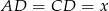AD = CD = x . Ponadto,

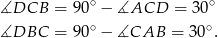
∡DCB = 90∘ − ∡ACD = 30 ∘ ∘ ∘ ∡DBC = 90 − ∡CAB = 30 .

To z kolei oznacza, że trójkąt 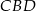CBD jest równoramienny, czyli 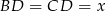BD = CD = x . Zatem AB = 2x oraz

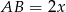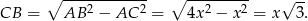
∘ ------------ ∘ --------- √ -- CB = AB 2 − AC 2 = 4x 2 − x2 = x 3.

Wartość x oraz pole obliczamy tak samo jak w pierwszym sposobie.  
Odpowiedź: √ -- 6 3 − 9

Wersja PDF