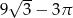Zadanie nr 1994437
Z punktu 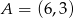 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 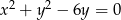 .
.
- Wyznacz równania tych stycznych.
- Oblicz odległość punktów styczności.
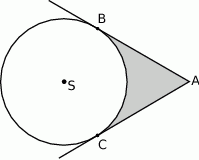
- Oblicz pole figury zaznaczonej na rysunku.
Rozwiązanie
Zacznijmy od ustalenia o jaki okrąg chodzi (jaki ma środek i promień).
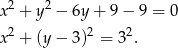
Jest więc okrąg o środku 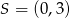 i promieniu 3. Teraz możemy dokładniej naszkicować opisaną sytuację.
i promieniu 3. Teraz możemy dokładniej naszkicować opisaną sytuację.
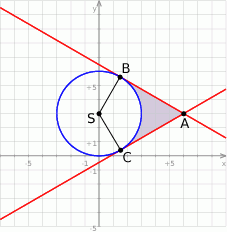
- Proste przechodzące przez punkt
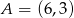 są postaci
są postaci 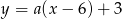 (z wyjątkiem pionowej prostej
(z wyjątkiem pionowej prostej 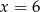 , ale widać, że ta nie jest styczną). Sprawdźmy kiedy taka prosta i okrąg mają dokładnie jeden punkt wspólny (wstawiamy
, ale widać, że ta nie jest styczną). Sprawdźmy kiedy taka prosta i okrąg mają dokładnie jeden punkt wspólny (wstawiamy 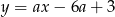 ) do równania okręgu.
) do równania okręgu. 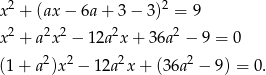
Współczynnik przy
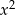 jest niezerowy, więc mamy równanie kwadratowe. Wystarczy zatem sprawdzić, kiedy
jest niezerowy, więc mamy równanie kwadratowe. Wystarczy zatem sprawdzić, kiedy 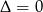 .
. 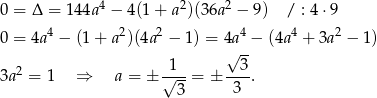
Wyznaczmy od razu punkty wspólne
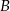 i
i 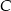 tych stycznych i okręgu (przyda nam się to w następnym podpunkcie).
tych stycznych i okręgu (przyda nam się to w następnym podpunkcie). 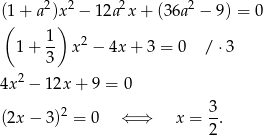
Zatem
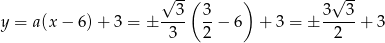
i punkty wspólne mają współrzędne
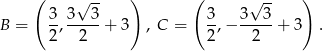
Odpowiedź: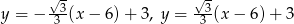
- W poprzednim podpunkcie obliczyliśmy współrzędne punktów styczności. Ponieważ obydwa leżą na pionowej prostej
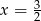 , ich odległość jest równa
, ich odległość jest równa 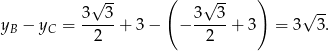
Odpowiedź: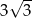
- Żądane pole figury obliczymy odejmując od pola czworokąta
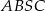 pole wycinka kołowego
pole wycinka kołowego 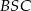 . Czworokąt
. Czworokąt 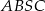 składa się z dwóch identycznych trójkątów
składa się z dwóch identycznych trójkątów 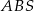 i
i 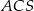 . Podstawa
. Podstawa 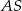 takiego trójkąta ma długość równą pierwszej współrzędnej punktu
takiego trójkąta ma długość równą pierwszej współrzędnej punktu 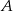 , czyli
, czyli 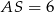 . Jego wysokość opuszczona na tę podstawę ma długość równą połowie długości odcinka
. Jego wysokość opuszczona na tę podstawę ma długość równą połowie długości odcinka 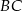 , wiec pole jest równe
, wiec pole jest równe 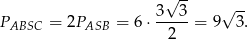
Do obliczenia pola wycinka
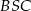 potrzebna nam jest znajomość miary kąta
potrzebna nam jest znajomość miary kąta 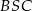 . Obliczmy najpierw miarę kąta
. Obliczmy najpierw miarę kąta 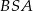 . Ponieważ trójkąt
. Ponieważ trójkąt 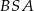 jest prostokątny (bo styczna jest prostopadła do promienia), mamy
jest prostokątny (bo styczna jest prostopadła do promienia), mamy 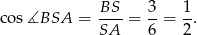
Zatem
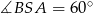 i
i 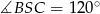 . Interesujące nas pole wycinka koła stanowi więc trzecią część pola całego koła, czyli
. Interesujące nas pole wycinka koła stanowi więc trzecią część pola całego koła, czyli 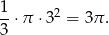
Możemy wreszcie policzyć pole figury opisanej w poleceniu,
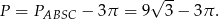
Odpowiedź: